Class E Power Amplifier

This article details the design of class E power amplifier.

Calculation

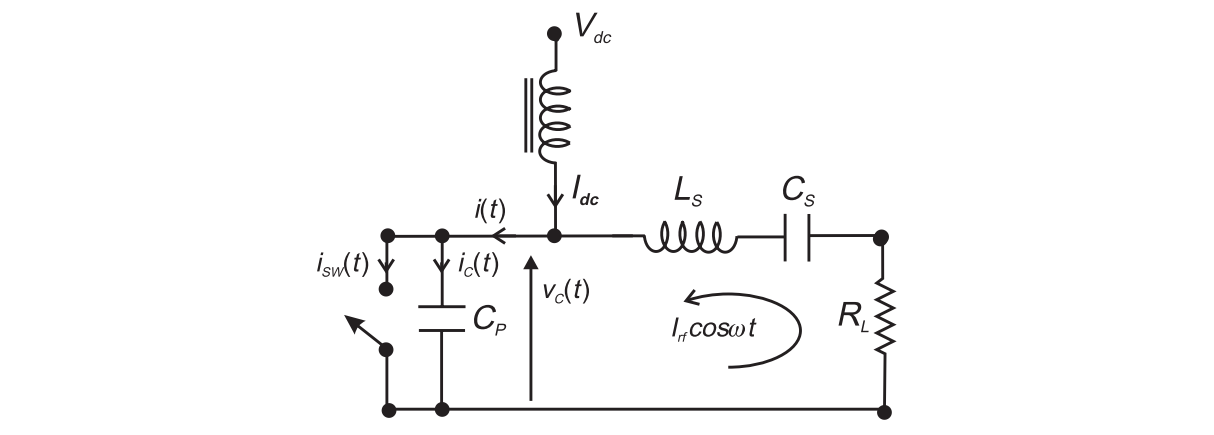
In the analysis, all the time variable $t$ is replaced with conduction angle $\theta$.

It is apparent that $i(\theta)$ is composed of two component, namely

$$i(\theta)=I_{dc}+I_{rf}\cos\theta$$

With the normalization $m=I_{rf}/I_{dc}$, we can write

$$i(\theta)=I_{dc}(1+m\cos\theta)$$

The current waveform is as follows

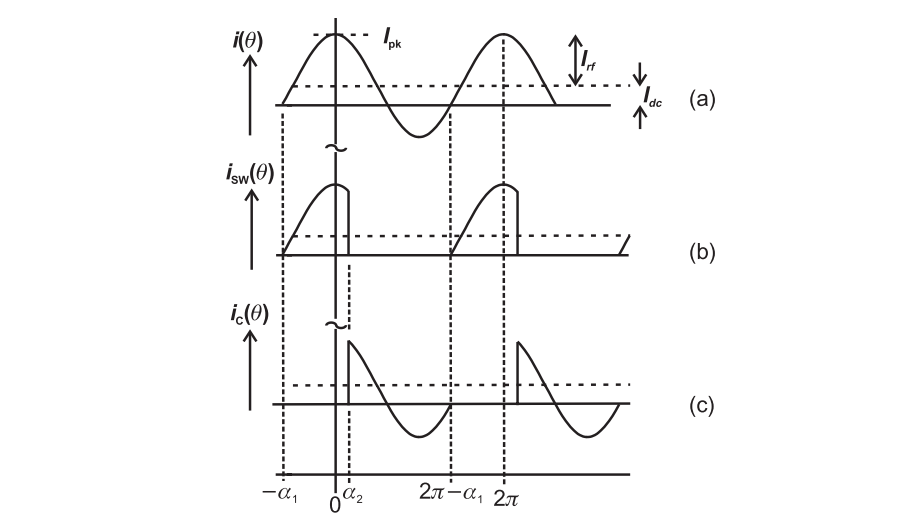
The switched transistor turn on from $-\alpha_1$ to $\alpha_2$, where all the current flow through the transistor, and thus the $i_{sw}(\theta)$ replicates $i(\theta)$. Similarly, for the duration from $\alpha_2$ till $2\pi-\alpha_2$.

The conduction angle is defined as

$$\phi=\alpha_1+\alpha_2$$

From the peak current, we have

$$I_{pk}=I_{dc}(1+m)$$

From the initial condition $I_{dc}(1+m\cos\alpha_1)=0$, we have

$$\cos\alpha_1=-\frac{1}{m}$$

Since the average current flow through the transistor equals to $I_{dc}$, we have

$$\frac{I_{dc}}{2\pi}\int_{-\alpha_1}^{\alpha_2} (1+m\cos\theta) \ d\theta=I_{dc}$$

Combined with aforementioned equations, it leads to

$$\sin\alpha_1=\frac{2\pi+\sin\phi-\phi}{m(1-\cos\phi)}$$

or

$$1+\left(\frac{2\pi+\sin\phi-\phi}{1-\cos\phi}\right)=m^2$$

or

$$(\alpha_1+\alpha_2)+m(\sin\alpha_1+\sin\alpha_2)=2\pi$$

where we established the connection between the conduction angle and the peak/average ratio. Note that this requirement also ensures that $\int_{\alpha_2}^{2\pi-\alpha_1} i_c(\theta) d\theta=0$ and $v_C(2\pi-\alpha_2)=0$.

The voltage can be written as

$$\begin{aligned} v_C(\theta)&=\frac{I_{dc}}{\omega C_p}\int_{\alpha_2}^{\theta} (1+m\cos\theta) \ d\theta\\ &=\frac{I_{dc}}{\omega C_p}(\theta+m\sin\theta-\alpha_2-m\sin\alpha_2)&&\alpha_2<\theta<2\pi-\alpha_1\\ &=0&&-\alpha_1<\theta<\alpha_2 \end{aligned}$$

The voltage waveform is as follows

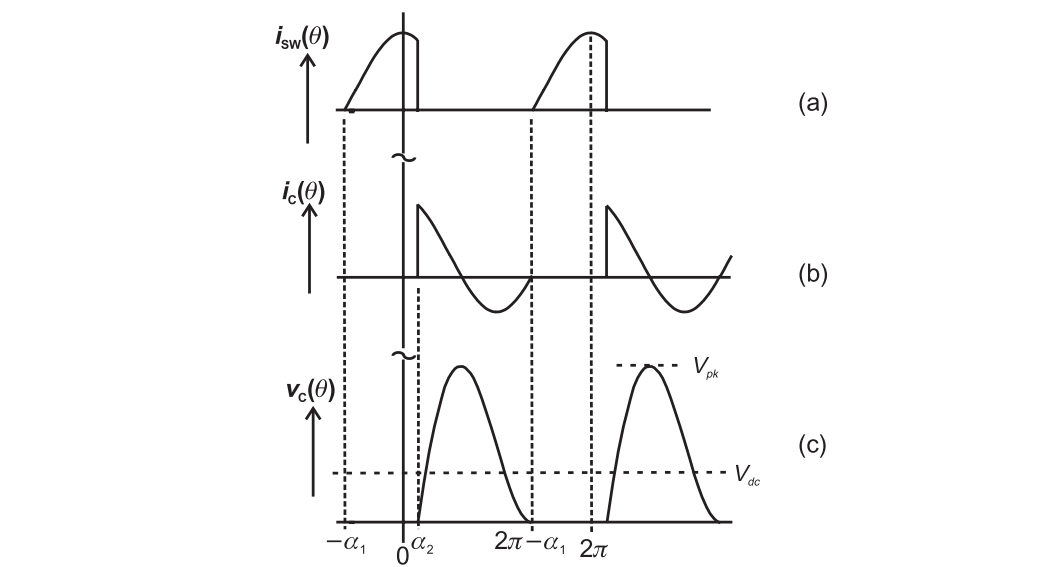
The average DC value is

$$\begin{aligned} V_{dc}&=\frac{I_{dc}}{2\pi\omega C_p}\int_{\alpha_2}^{2\pi-\alpha_1}(\theta+m\sin\theta-\alpha_2-m\sin\alpha_2)d\theta\\ &=\frac{I_{dc}}{2\pi\omega C_p}\cdot\frac{m}{2}[m(\sin^2\alpha_1-\sin^2\alpha_2)+2(\cos\alpha_2-\cos\alpha_1)] \end{aligned}$$

The in-phase component

$$\begin{aligned} V_{ci}&=\frac{I_{dc}}{\pi\omega C_p}\int_{\alpha_2}^{2\pi-\alpha_1}(\theta+m\sin\theta-\alpha_2-m\sin\alpha_2)\cos\theta\ d\theta\\ &=-\frac{I_{dc}}{\pi\omega C_p}\cdot\frac{1}{2}[m(\sin^2\alpha_1-\sin^2\alpha_2)+2(\cos\alpha_2-\cos\alpha_1)] \end{aligned}$$

The quadrature component

$$\begin{aligned} V_{cq}&=\frac{I_{dc}}{\pi\omega C_p}\int_{\alpha_2}^{2\pi-\alpha_1}(\theta+m\sin\theta-\alpha_2-m\sin\alpha_2)\sin\theta\ d\theta\\ &=\frac{I_{dc}}{\pi\omega C_p}\cdot\frac{1}{2}[(m^2-2)(\sin\alpha_1+\sin\alpha_2)-\frac{m}{2}(\sin2\alpha_1+\sin2\alpha_2)] \end{aligned}$$

Power deliver to the load is therefore

$$P_{rf}=\frac{1}{2}\mathrm{Re}[V\cdot I^*]=-\frac{1}{2}I_{pk}\cdot V_{ci}$$

and the DC power consumption is

$$P_{dc}=I_{dc}\cdot V_{dc}$$

The two are identical, and thus the efficiency is 100%.

To calculate the required output impedance

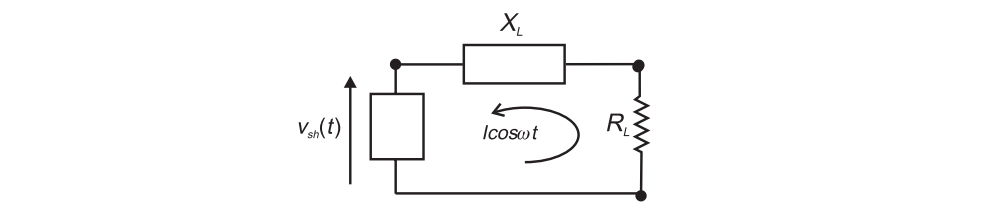
we may write

$$V_{ci}\sin\omega t+V_{cq} \sin\omega t+I(R_L\cos\omega t-X_L\sin\omega t)=0$$

Real and imaginary parts are

$$R_L=-\frac{V_{ci}}{I},X_L=\frac{V_{cq}}{I}$$

where $I=mI_{dc}$.

Design Consideration

The peak voltage is

$$V_{pk}=\frac{I_{dc}}{\omega C_p}(\alpha_1+m\sin\alpha_1-\alpha_2-m\sin\alpha_2)$$

The peak current is

$$I_{pk}=I_{dc}(1+m)$$

Thus, equivalent class A PA can deliver a power of

$$P_{A}=\frac{1}{2}\frac{V_{pk}}{2}\frac{I_{pk}}{2}=\frac{1}{8}V_{pk}I_{pk}$$

It can be demonstrated that as the conduction angle increases, both the voltage peak-to-average ratio and the PUF (Power Utilization Factor, compared to class A PA with the same $V_{pk}$ and $I_{pk}$) increases.

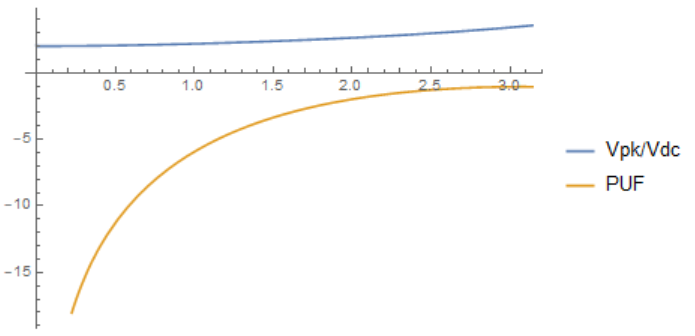
The Mathematica code is as follows

a1 = ArcTan[-((2 Pi + Sin[phi] - phi)/(1 - Cos[phi]))] + Pi;
a2 = phi - a1;
m = -1/Cos[a1];
Vpk = (a1 - a2 + m (Sin[a1] - Sin[a2]));
Vdc = (1/2/Pi) (m/2) (m (Sin[a1]^2 - Sin[a2]^2) + 
     2 (Cos[a2] - Cos[a1]));
Ipk = m + 1;
Pa = 1/8 Vpk Ipk;
Pe = Vdc;
Plot[{Vpk/Vdc, 10 Log10[Pe/Pa]}, {phi, 0, Pi}, 
 PlotLegends -> {"Vpk/Vdc", "PUF"}]

Required load

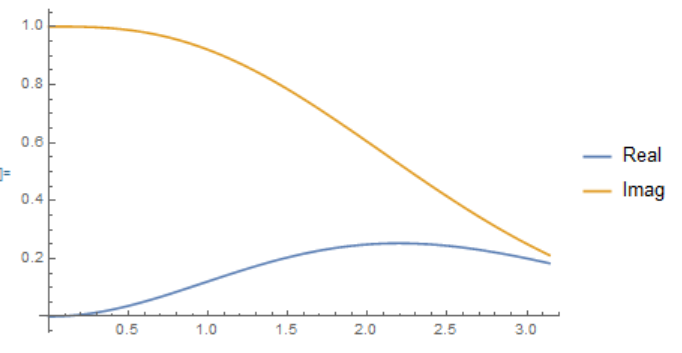
The Mathematica code is as follows

a1 = ArcTan[-((2 Pi + Sin[phi] - phi)/(1 - Cos[phi]))] + Pi;
a2 = phi - a1;
m = -1/Cos[a1];
Vci = -1/2/Pi (m (Sin[a1]^2 - Sin[a2]^2) + 2 (Cos[a2] - Cos[a1]));
Vcq = 1/2/
    Pi ((m^2 - 2) (Sin[a1] + Sin[a2]) - m/2 (Sin[2 a1] + Sin[2 a2]));
Plot[{-Vci/m, Vcq/m}, {phi, 0, Pi}, PlotLegends -> {"Real", "Imag"}]

Design Example

Steps

1. Choose the conduction angle $\phi$, and calculate normalized parameters. For instance, for a conduction angle of 125°.

   a1 = ArcTan[-((2 Pi + Sin[phi] - phi)/(1 - Cos[phi]))] + Pi;
   a2 = phi - a1;
   m = -1/Cos[a1];
   Vdc = (1/2/Pi) (m/2) (m (Sin[a1]^2 - Sin[a2]^2) + 
        2 (Cos[a2] - Cos[a1]));
   Ipk = m + 1;
   Vci = -1/2/Pi (m (Sin[a1]^2 - Sin[a2]^2) + 2 (Cos[a2] - Cos[a1]));
   Vcq = 1/2/
       Pi ((m^2 - 2) (Sin[a1] + Sin[a2]) - m/2 (Sin[2 a1] + Sin[2 a2]));
   Rl = -Vci/m;
   Xl = Vcq/m;
   {Vdc, Ipk, Rl, Xl} /. phi -> 125/180 Pi // N
   (* result: {1.36071, 4.28307, 0.252485, 0.532716} *)

2. Scaling the parameters

   1. Scale the $I_{pk}$ by $I_{dc}$
   2. Scale the $V_{dc}$ by $I_{dc}/(\omega C_p)$
   3. Scale the impedances by $1/(\omega C_p)$

   For instance, for a actual $I_{pk}=1,V_{dc}=4.8$, the voltage need to be scaled by 4.8/1.36, the current need to be scaled by 1/4.28, and the impedances need to be scaled by 15.1.

Verification

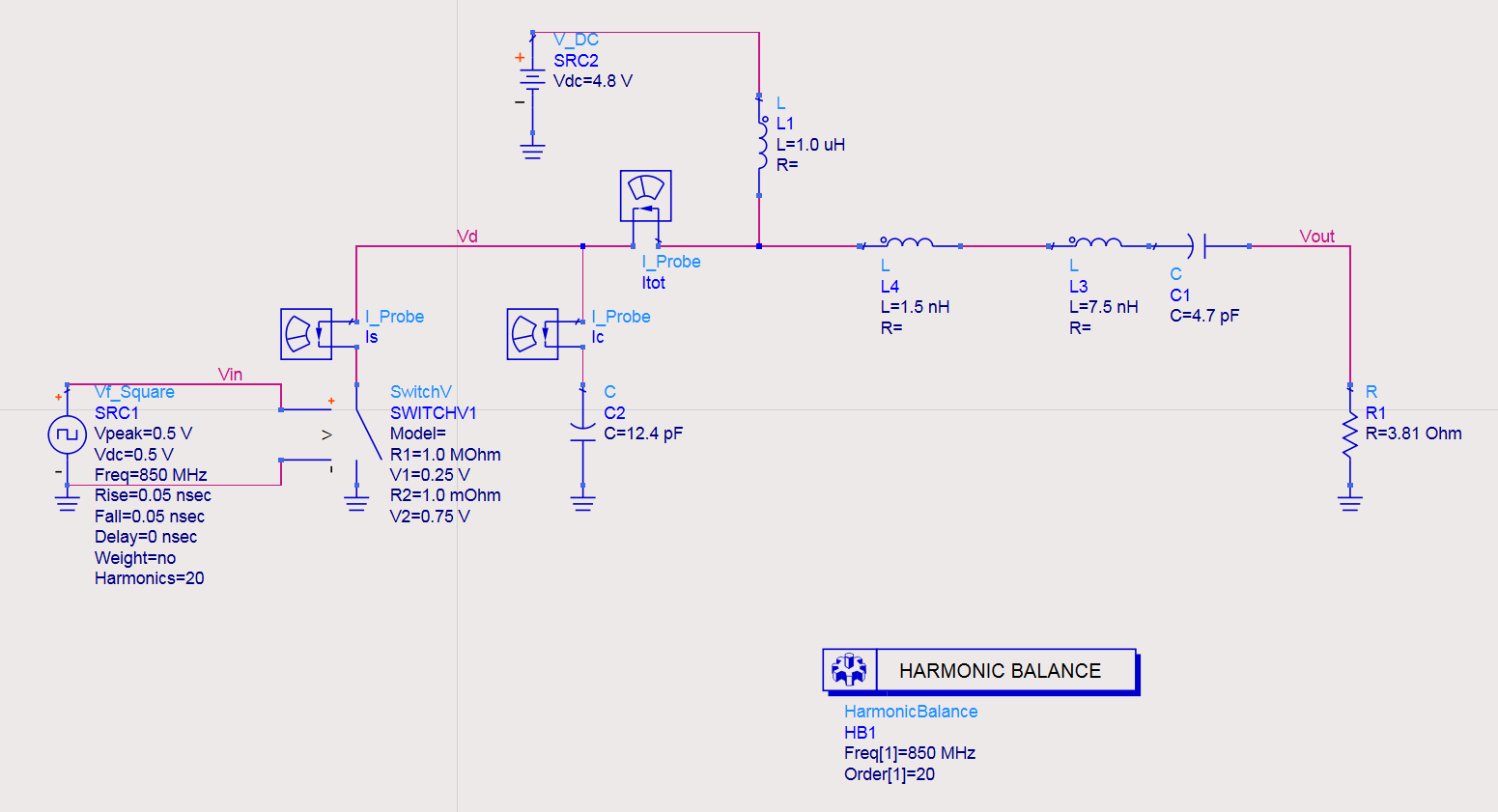
The simulation results are as follows:

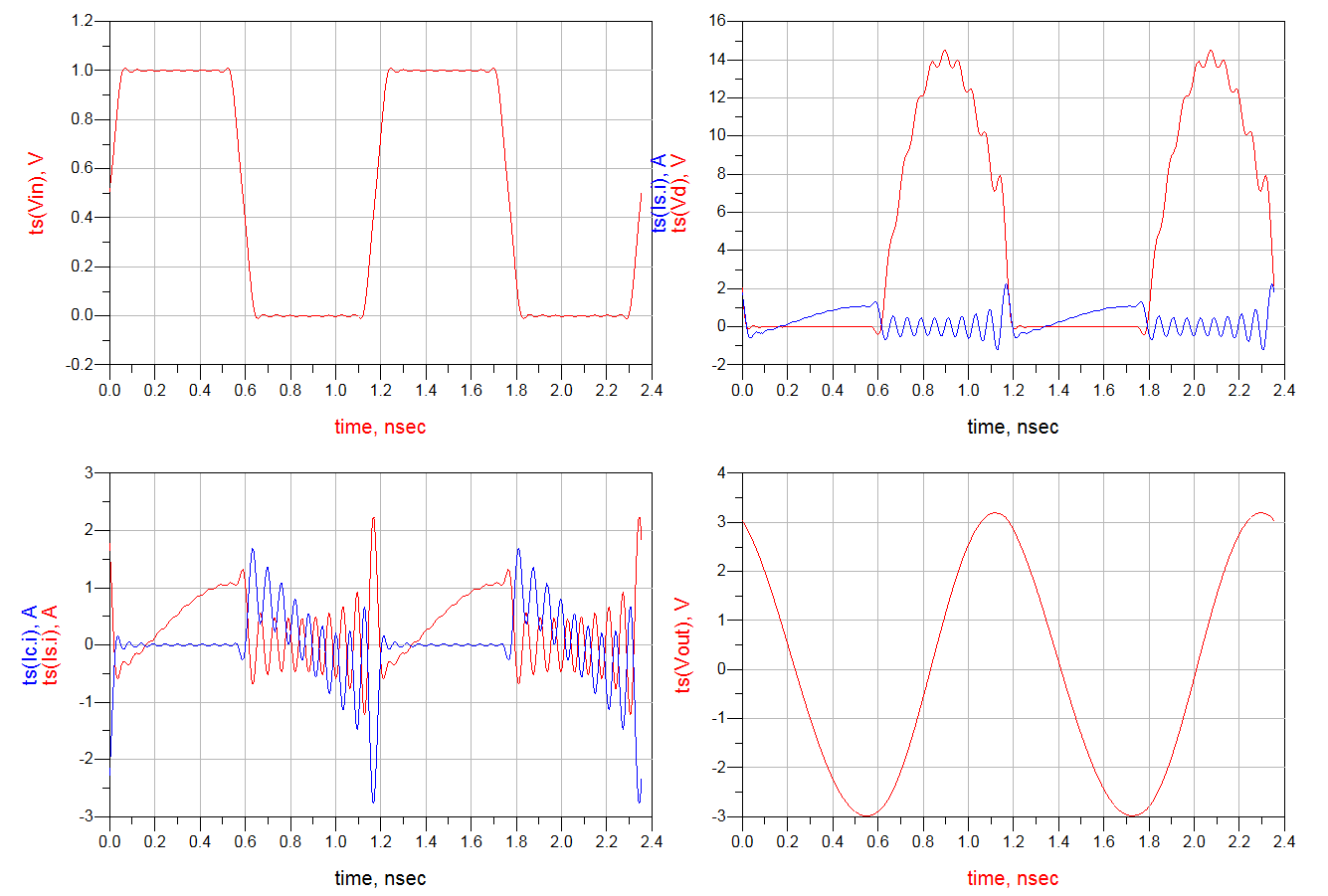
The oscillating problem can be alleviated by reducing the capacitor from 12.4 pF to 10.4 pF.

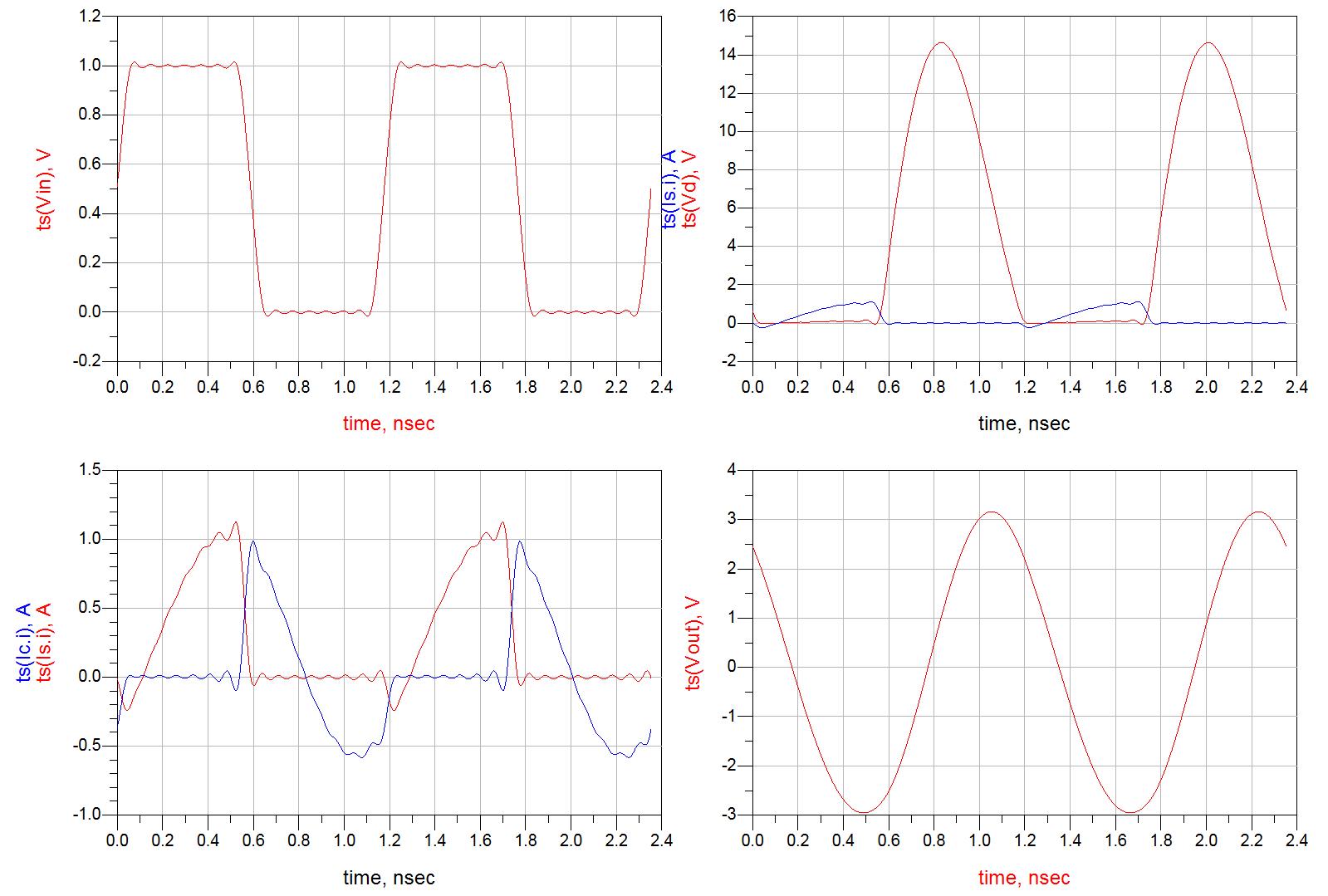
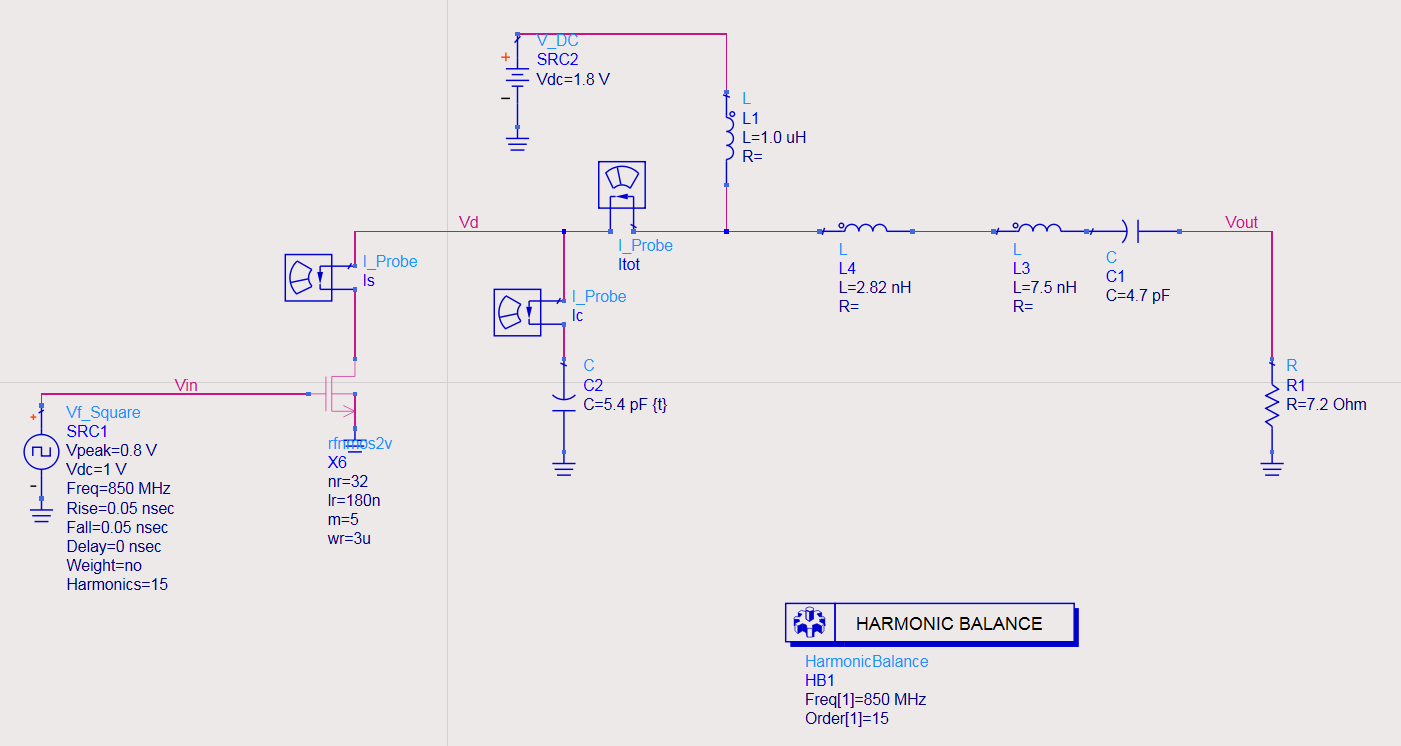
If we adopt a real transistor

The simulated performance is

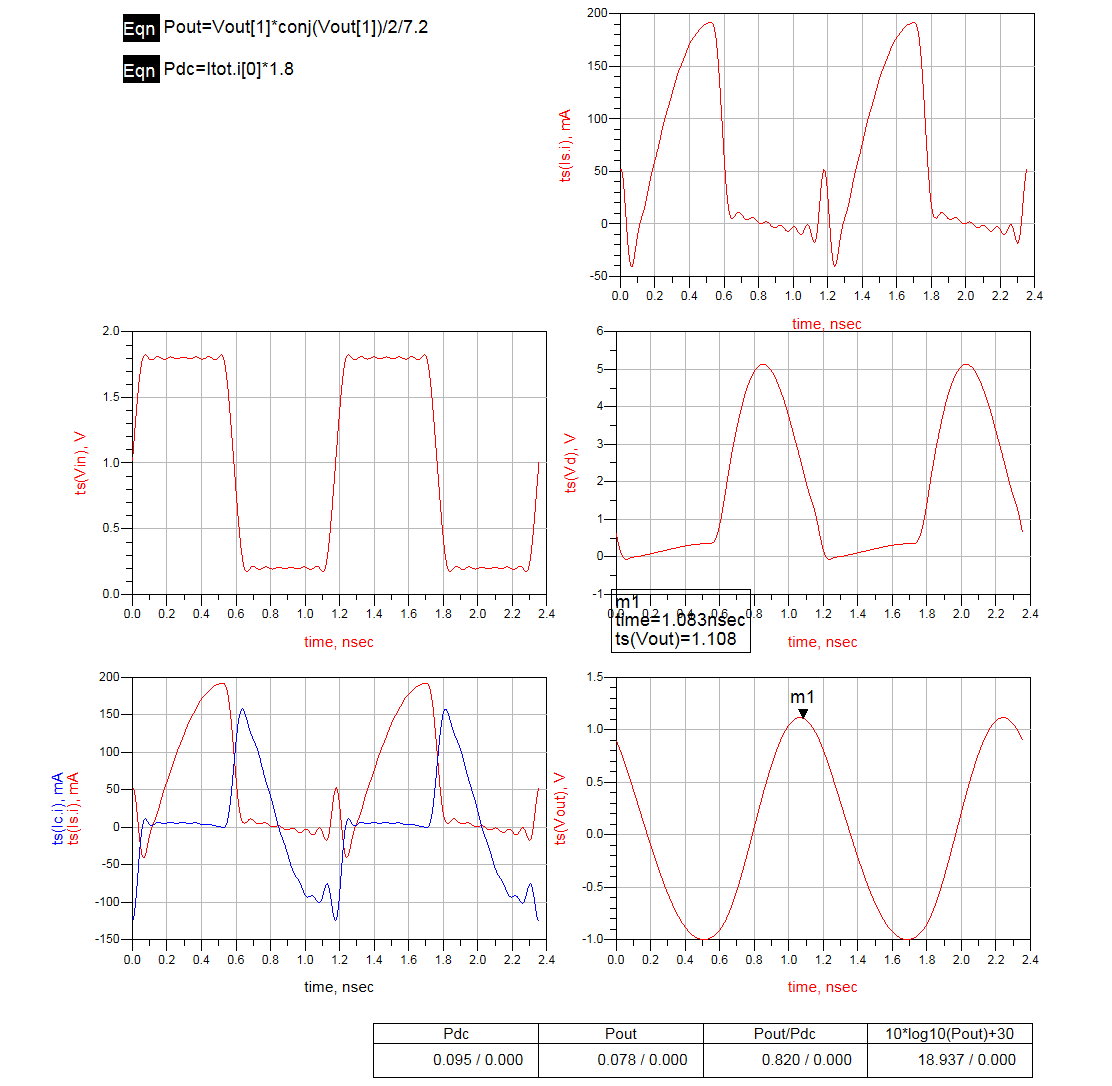
It delivers 19 dBm output power with DE of 82% at 850 MHz.

Reference

1. S. C. Cripps. RF Power Amplifier for Wireless Communications. Artech House, 2014.