Feedback System Analysis

This article intends to deal with the analysis of feedback systems.

General Consideration

A negative feedback system is as follows

$$Y(s)=H(s)[X(s)-G(s)Y(s)]$$

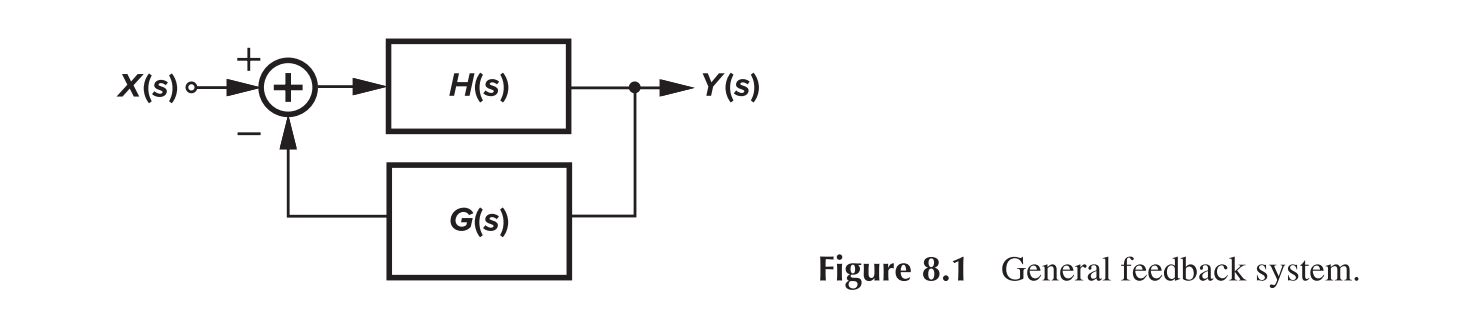
Reorganize the items, we have

$$\frac{Y(s)}{X(s)}=\frac{H(s)}{1+G(s)H(s)}$$

$H(s)$ is called the open-loop gain, while $H(s)G(s)$ is called the loop gain, and $Y(s)/X(s)$ is called the closed-loop transfer function. The loop gain can be obtained by

1. Set the main input to zero
2. Break the loop at some point
3. Inject a test signal in the correct direction
4. Follow the loop and obtain the value that returns to the break point
5. The negative of the transfer function is the loop gain

Assume $H(s)=A, G(s)=\beta$, we have

$$\frac{Y}{X}=\frac{A}{1+\beta A}\approx\frac{1}{\beta}\left(1-\frac{1}{\beta A}\right)$$

Thus, for negative-feedback system, as long as $\beta A$ is large enough, the closed loop gain is determined by the feedback coefficient.

1. Bandwidth: for one pole gain $A(s)=\frac{A_0}{1+s/\omega_0}$, the transfer function is $Y(s)/X(s)=\frac{A_0/(1+\beta A_0)}{1+s/[(1+\beta A_0)\omega_0]}$, and thus the bandwidth is extended by the loop gain, leaving the GBW unchanged.
2. Nonlinearity: reduced

Types of Amplifiers

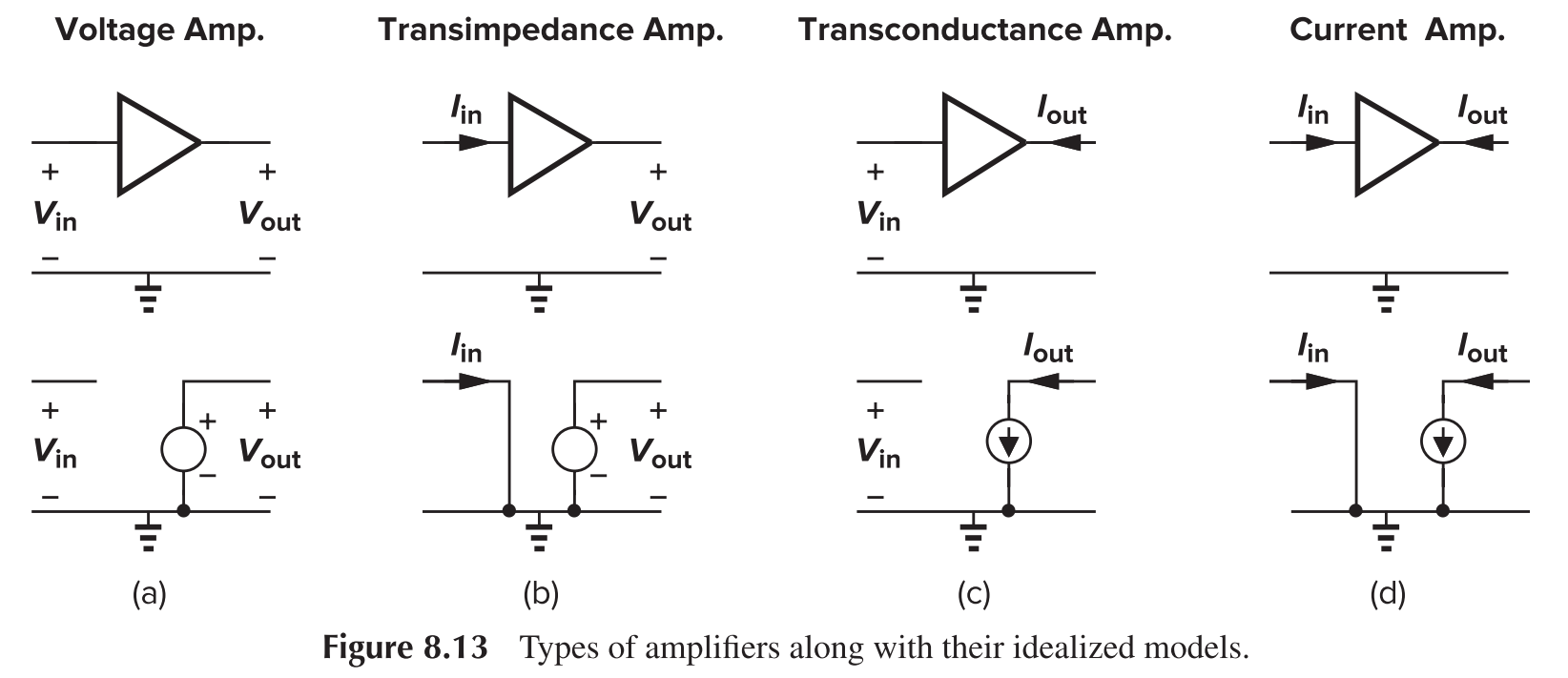
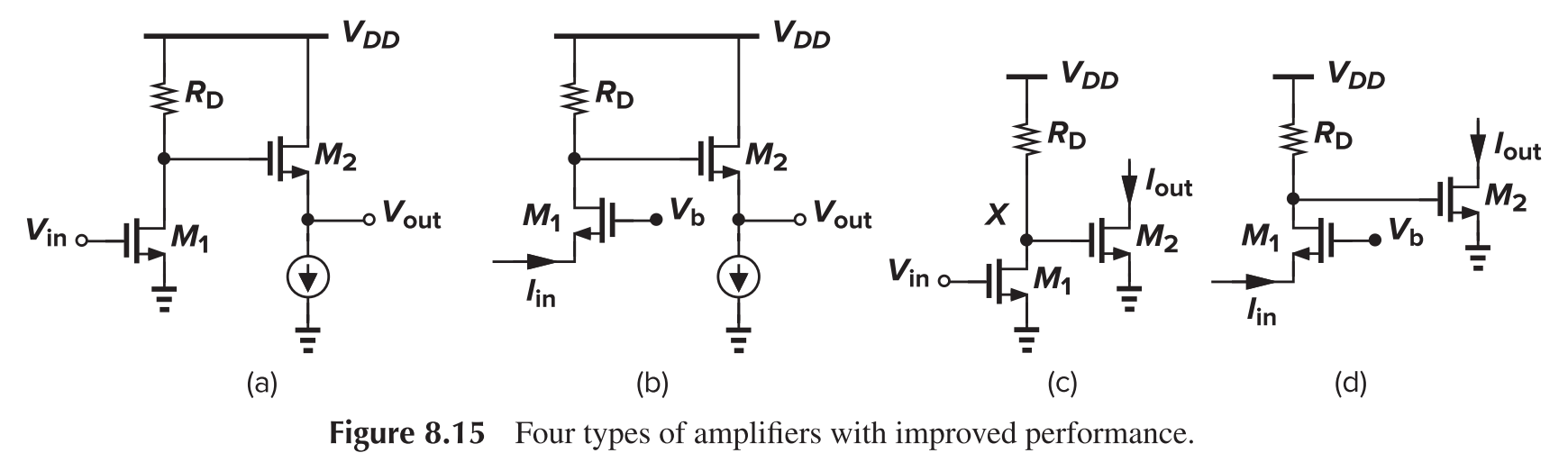
Corresponding implementation

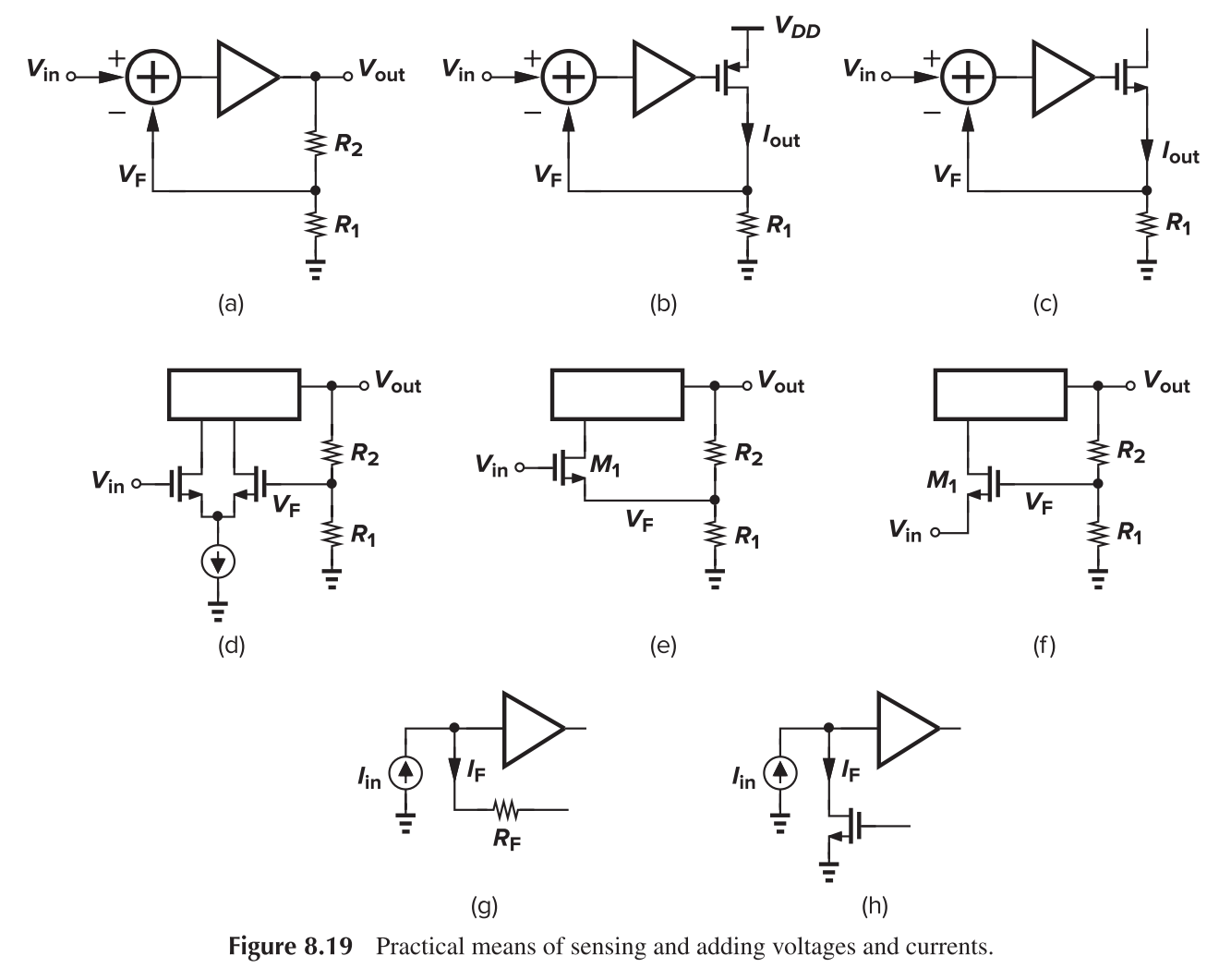
Sensing and Return Mechanism

Input and Output Impedance

Voltage-Voltage Feedback

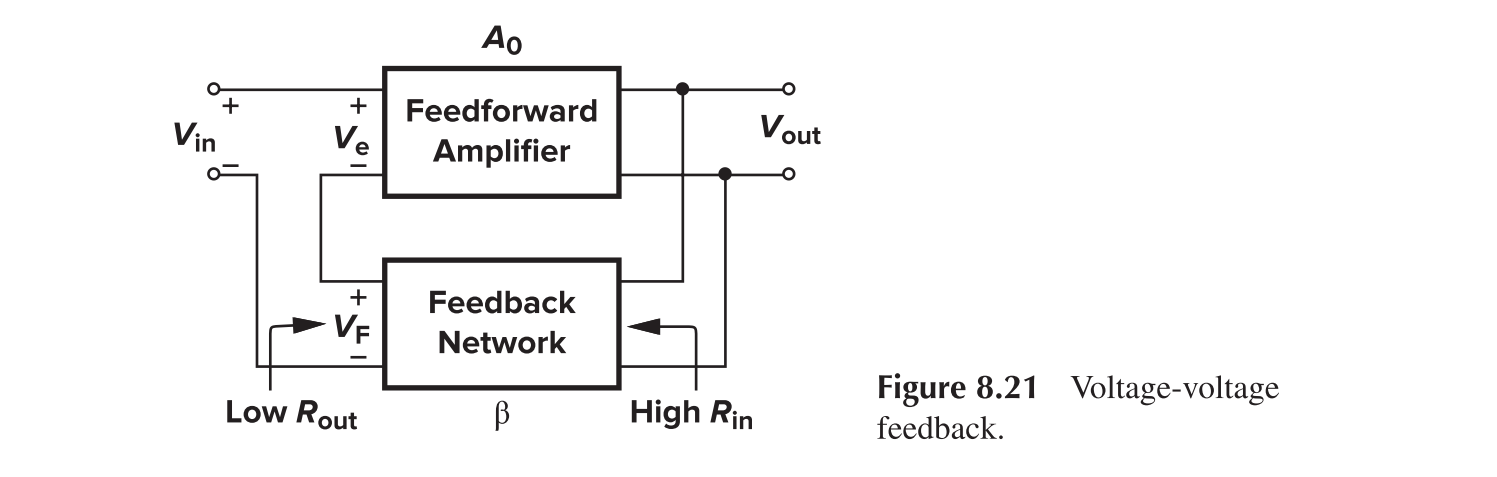
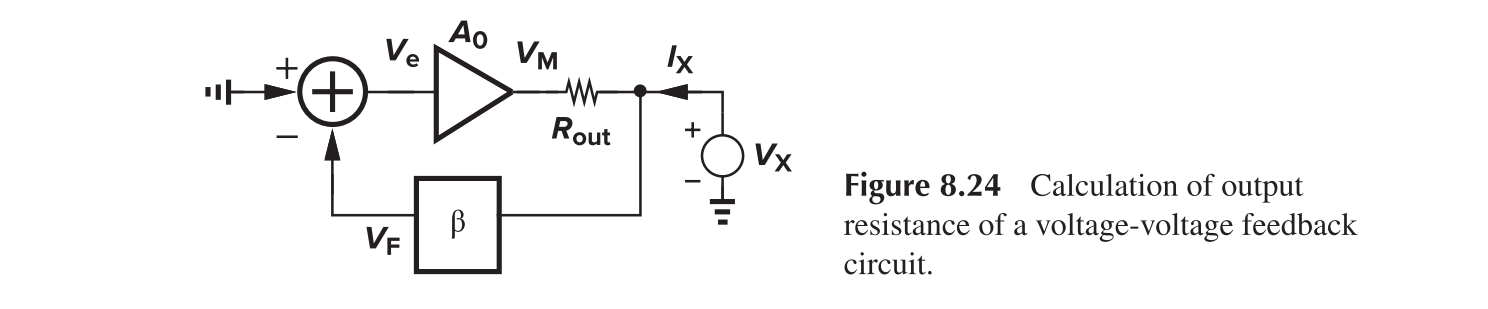
For the output impedance

Assume that feedback network draws no current

$$Z_{out}=\frac{R_{out}}{1+\beta A_0}$$

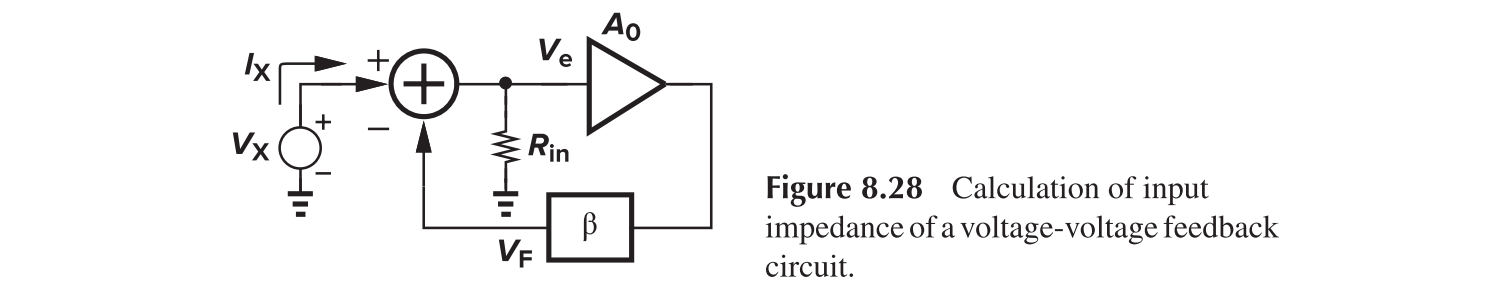
For the input impedance

$$Z_{in}=R_{in}(1+\beta A_0)$$

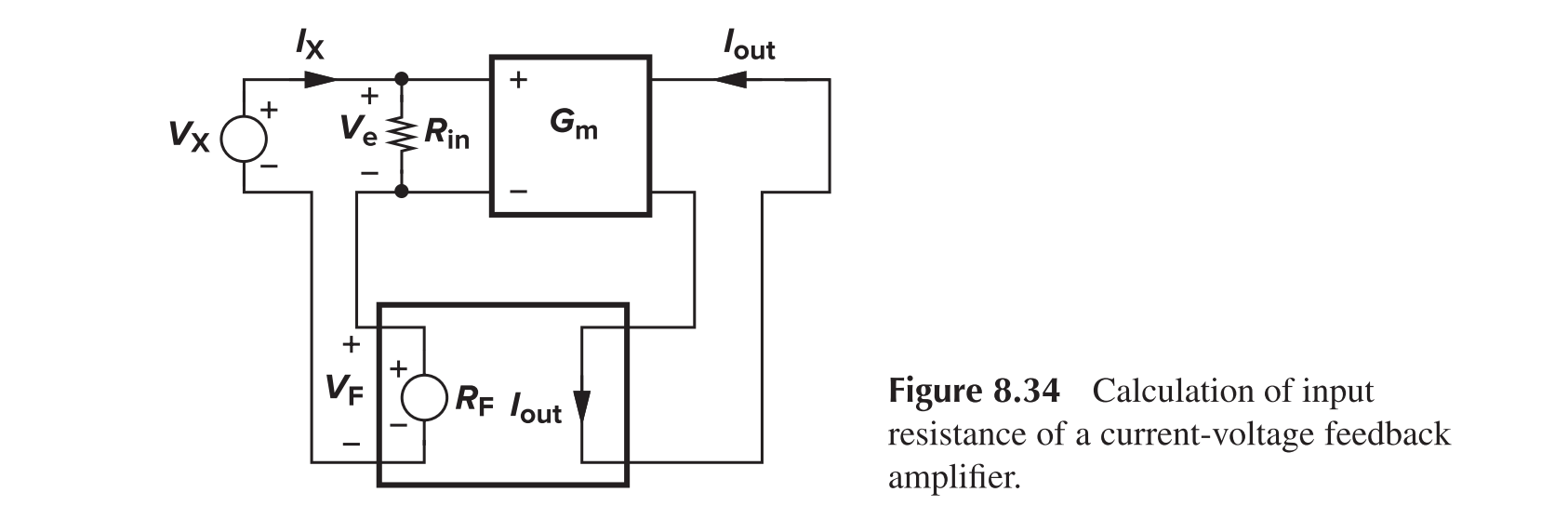
Current-Voltage Feedback

$$\frac{I_{out}}{V_{in}}=\frac{G_m}{1+G_mR_F}$$

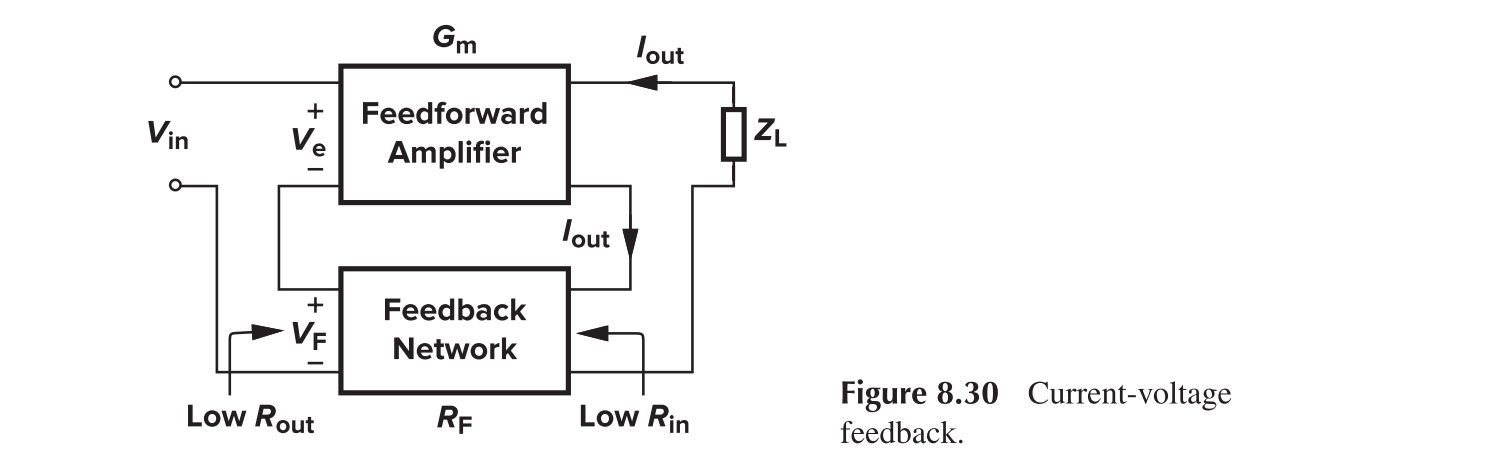
For the output impedance

$$Z_{out}=R_{out}(1+G_mR_F)$$

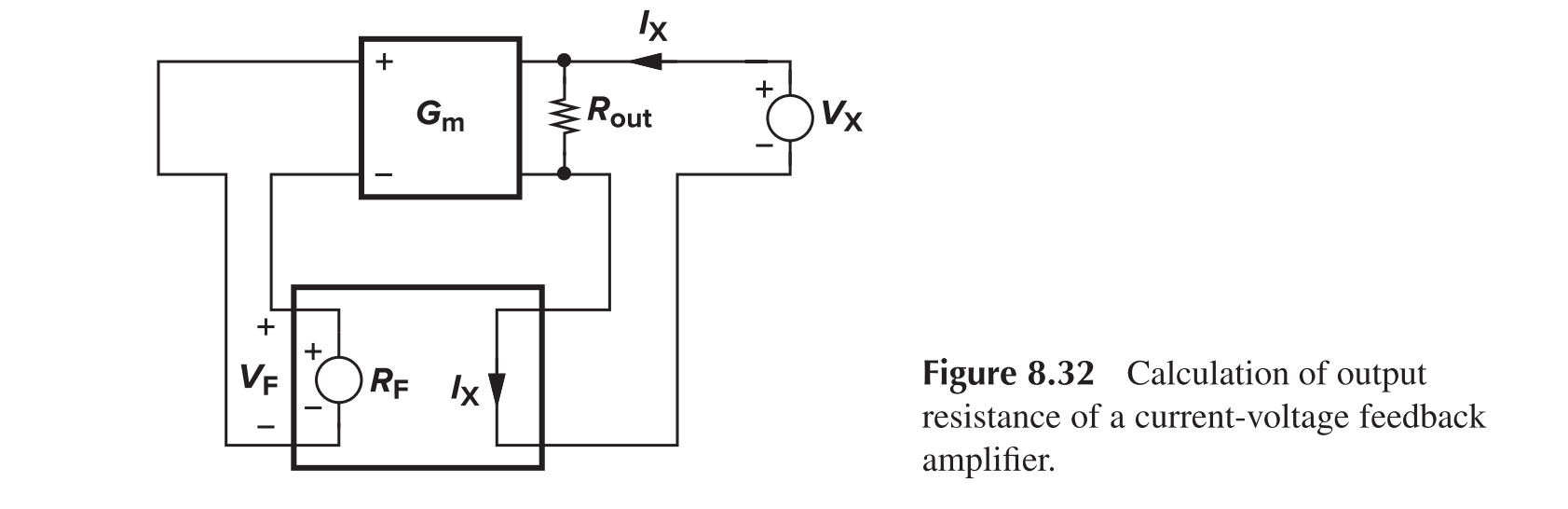
For the input impedance

$$Z_{in}=R_{in}(1+G_mR_F)$$

Voltage-Current Feedback

$$\frac{V_{out}}{I_{in}}=\frac{R_0}{1+g_{mF}R_0}$$

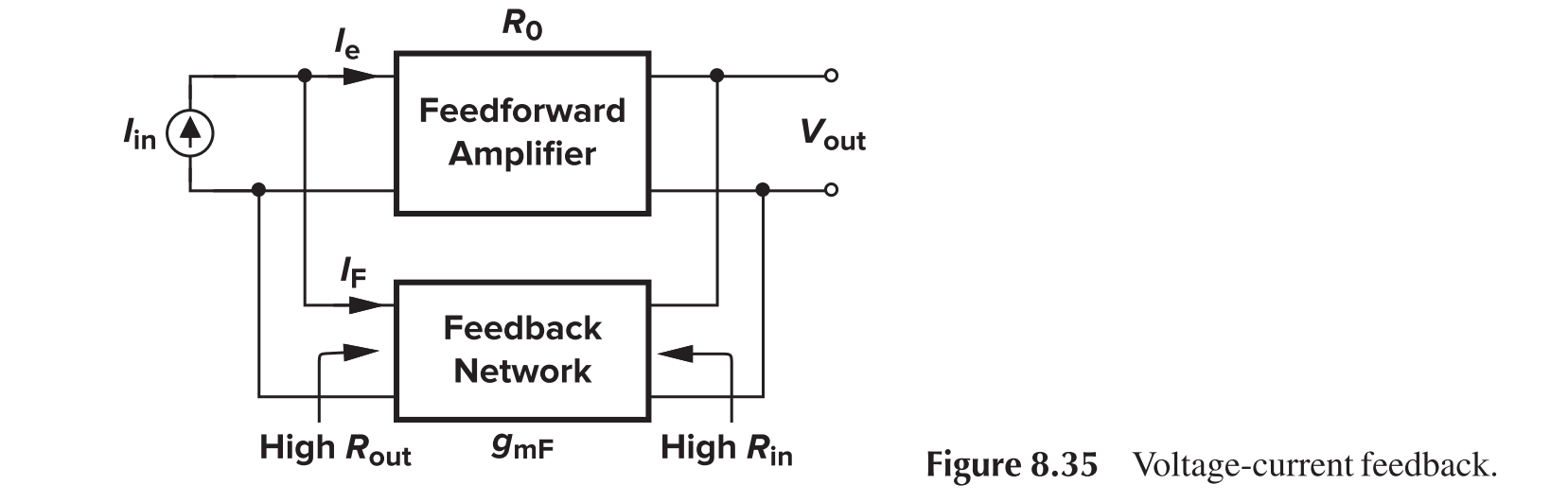
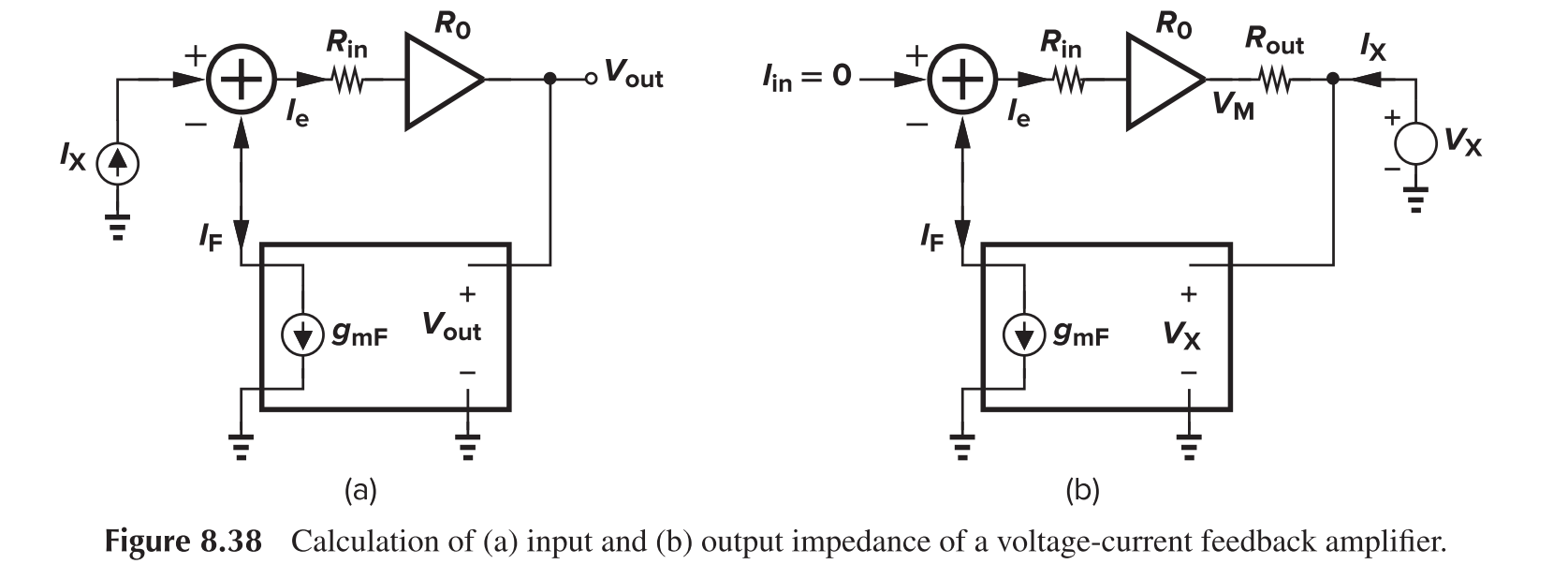
For the output impedance

$$Z_{out}=\frac{R_{out}}{1+g_{mF}R_0}$$

For the input impedance

$$Z_{in}=\frac{R_{in}}{1+g_{mF}R_0}$$

This topology has application in fiber optic receivers, where light is converted to electrical current through a reverse-biased diode. A transimpedance amplifier (TIA) is adopted to convert this current signal into voltage signal.

Current-Current Feedback

$$\frac{I_{out}}{I_{in}}=\frac{A_I}{1+\beta A_I}$$

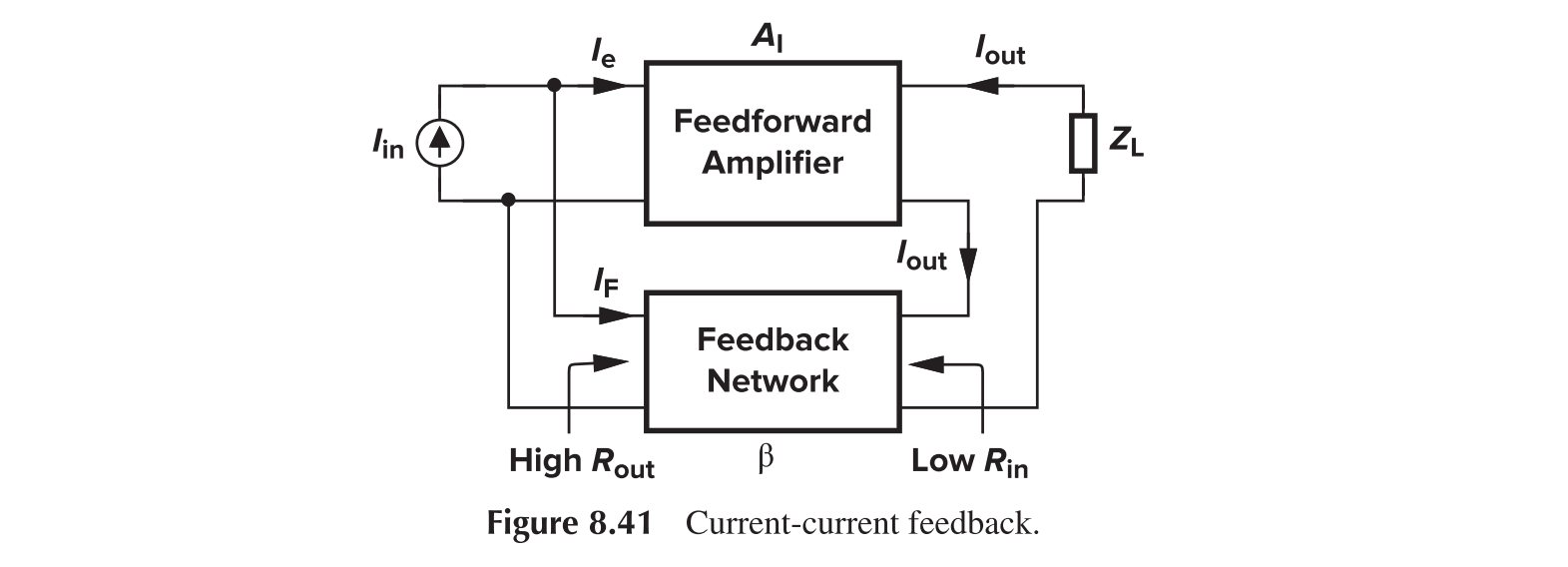
For the output impedance

$$Z_{out}=R_{out}(1+\beta A_I)$$

For the input impedance

$$Z_{in}=\frac{R_{in}}{1+\beta A_I}$$

Limitations of the Simple Analysis

What is loading effect?

The non-ideal input and output impedance of the feedback network could degrade the open-loop gain.

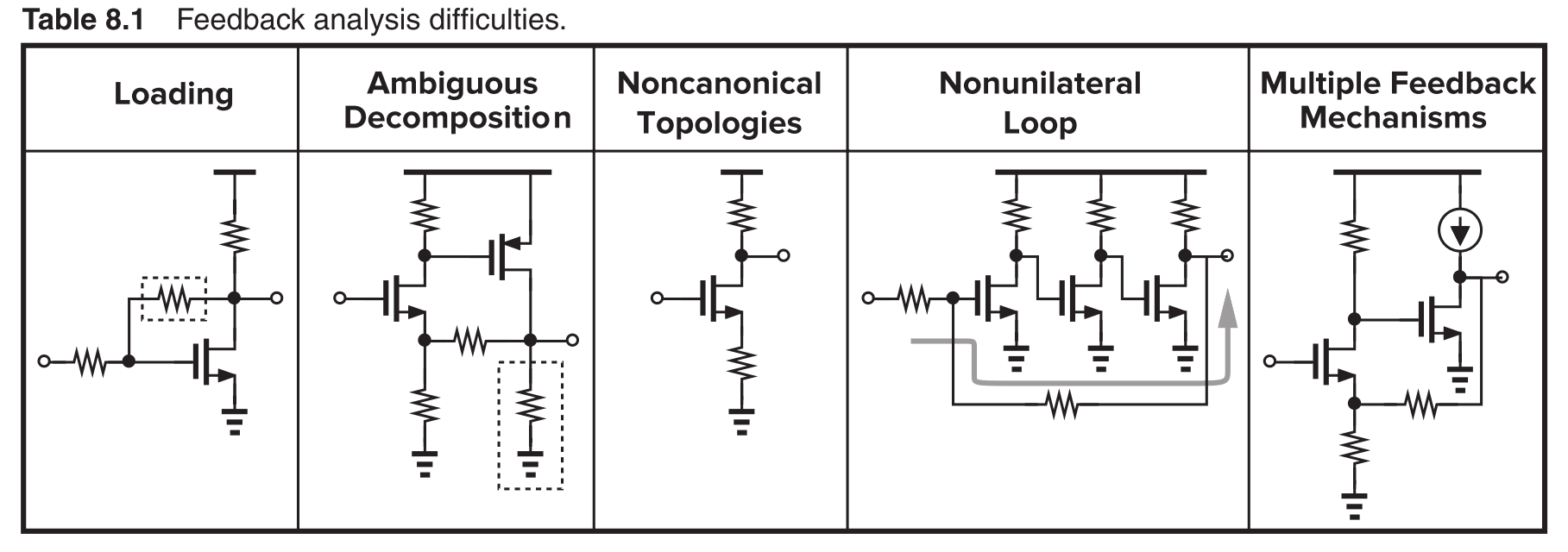
Possible methods

Two Port Models

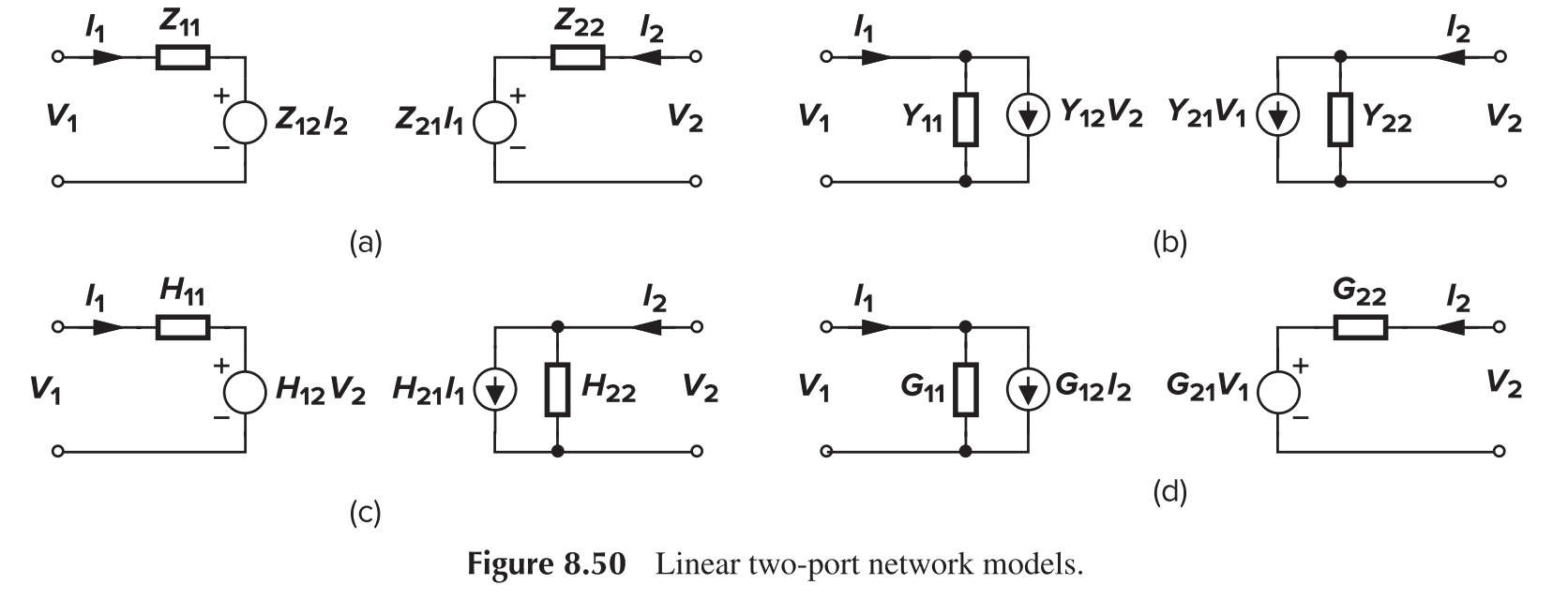
Z

$$\left\{ \begin{aligned} V_1=Z_{11}I_1+Z_{12}I_2\\ V_2=Z_{21}I_1+Z_{22}I_2 \end{aligned} \right.$$

Y

$$\left\{ \begin{aligned} I_1=Y_{11}V_1+Y_{12}V_2\\ I_2=Y_{21}V_1+Y_{22}V_2 \end{aligned} \right.$$

H

$$\left\{ \begin{aligned} V_1=H_{11}I_1+H_{12}V_2\\ I_2=H_{21}I_1+H_{22}V_2 \end{aligned} \right.$$

G

$$\left\{ \begin{aligned} I_1=G_{11}V_1+G_{12}I_2\\ V_2=G_{21}V_1+G_{22}I_2 \end{aligned} \right.$$

Voltage-Voltage Feedback

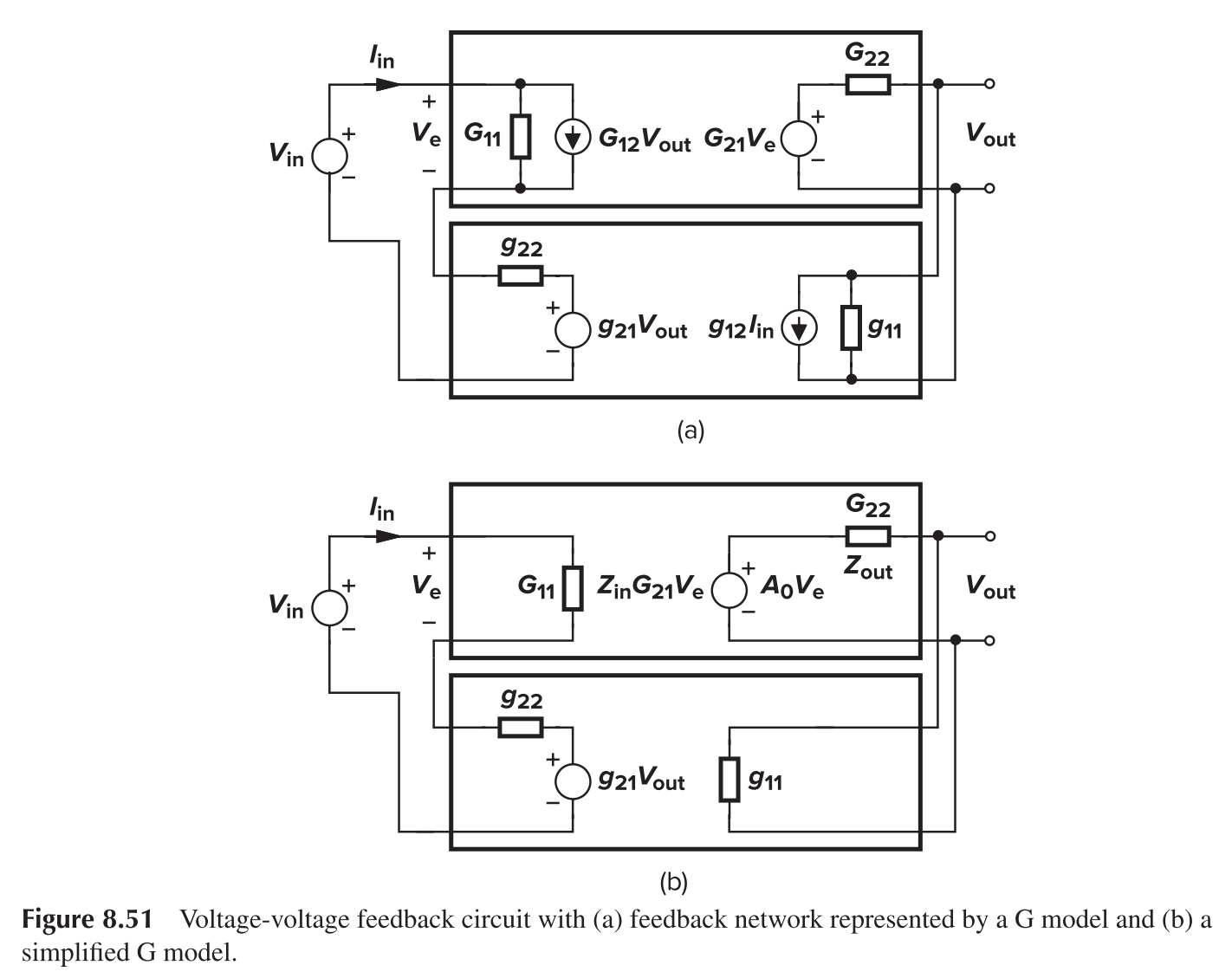
We have

$$\begin{aligned} \frac{V_{out}}{V_{in}}&=\frac{A_0}{(1+\frac{g_{22}}{Z_{in}})(1+g_{11}Z_{out})+g_{21}A_0}\\ &=\frac{A_{v,open}}{1+g_{21}A_{v,open}} \end{aligned}\\ A_{v,open}=\frac{A_0}{(1+\frac{g_{22}}{Z_{in}})(1+g_{11}Z_{out})}\\ g_{11}=\frac{I_1}{V_1}\bigg|_{I2=0}\\ g_{22}=\frac{V_1}{I_1}\bigg|_{V1=0}$$

For that matter, the $A_{v,open}$ should be calculated using the configuration

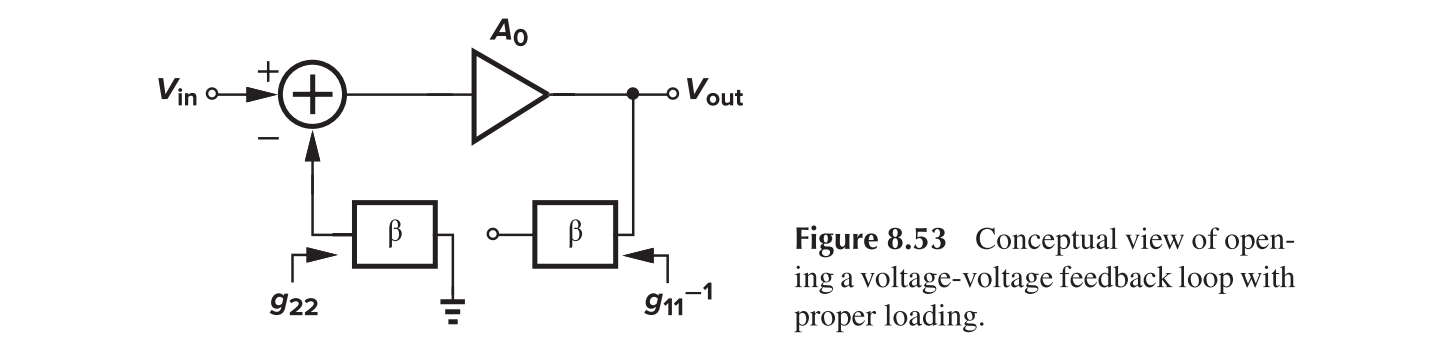
Summary

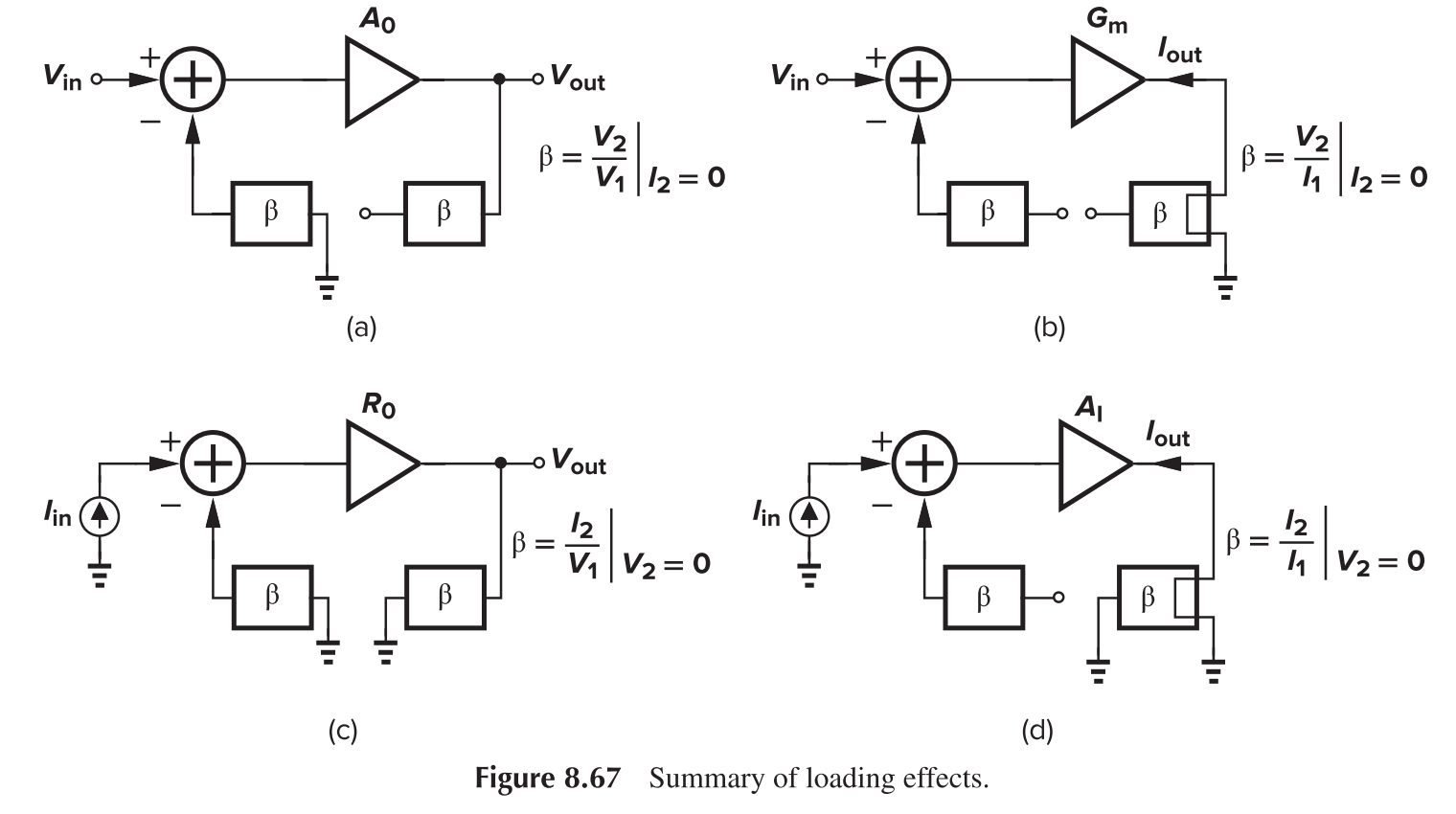
To calculate the gain with the loading effect, the procedure is as follows:

1. Open the loop with proper loading and calculate the open-loop gain $A_{OL}$
2. Determine the feedback ratio $\beta$
3. Calculate the closed-loop gain with $A_{OL}/(1+\beta A_{OL})$

Bode's Analysis

$$\left\{ \begin{aligned} V_{out}&=AV_{in}+BI_1\\ V_1&=CV_{in}+DI_1 \end{aligned} \right.$$

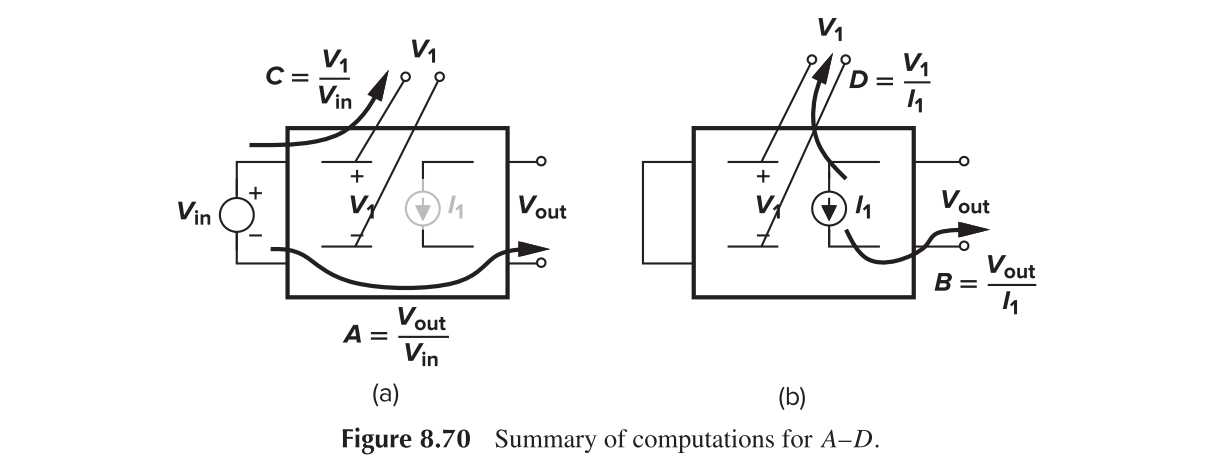
Assume $I_1=g_mV_1$, we have

$$\frac{V_{out}}{V_{in}}=A+\frac{g_mBC}{1-g_mD}$$

The return ratio (RR) is defined as $-g_mD$.

The procedure

1. Disable the transistor and by setting $g_m=0$ and obtain A and C
2. Set input to zero and calculate B and D
3. Solve the $A_v$ with above equations

Blackman's Theorem

$$\left\{ \begin{aligned} V_{in}&=AI_{in}+BI_1\\ V_1&=CI_{in}+DI_1 \end{aligned} \right.$$

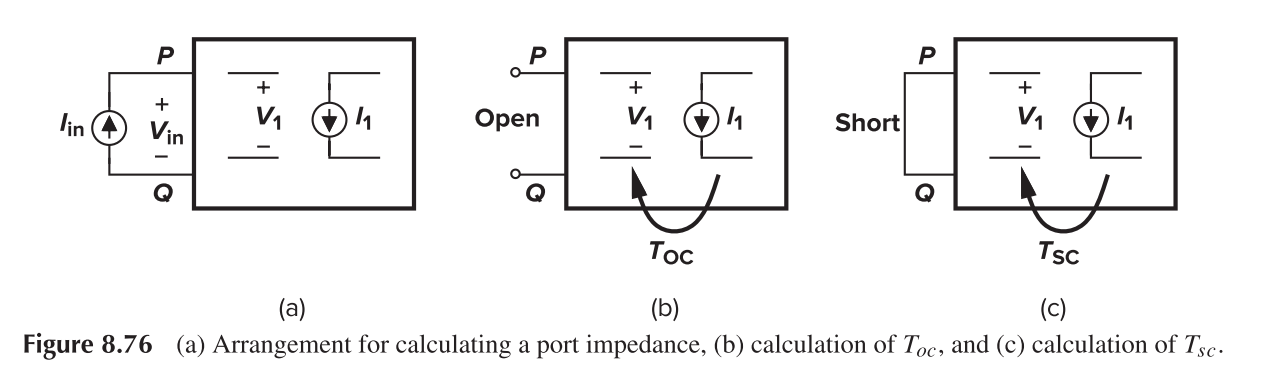
It follows that

$$\frac{V_{out}}{I_{in}}=A+\frac{g_mBC}{1-g_mD}$$

If we define two quantities

$$T_{oc}=-g_m\frac{V_1}{I_1}\bigg|_{I_{in}=0}=-g_mD\\ T_{sc}=-g_m\frac{V_1}{I_1}\bigg|_{V_{in}=0}=-g_m\frac{AD-BC}{A}$$

And therefore

$$Z_{in}=\frac{V_{out}}{I_{in}}=A\frac{1+T_{sc}}{1+T_{oc}}$$

Stability Consideration

Consider again the closed-loop transfer function

$$\frac{Y(s)}{X(s)}=\frac{H(s)}{1+G(s)H(s)}$$

If $G(s)H(s)=-1$, the gain goes to infinity. This is the condition of instability, which can be equivalently expressed as

$$|\beta H(j\omega_1)|=1\\ \angle\beta H(j\omega_1)=-180^\circ$$

which are called “Barkhausen’s Criteria.” We introduce several notions:

• Gain Crossover Frequency: The frequency when open-loop gain reduces to 1 (0 dB), denoted as GX.
• Phase Crossover Frequency: The frequency when the phase of open-loop gain reduces to $-180^\circ$, denoted as PX.
• Phase Margin: Defined as $180^\circ+\angle\beta H (f=GX)$, denoted as PM.

If $\text{PM}=60^\circ$, we have

$$\left|\frac{Y(s)}{X(s)}\right|=\frac{H(s)}{\left|1+\exp(-j\frac{2\pi}{3})\right|}=H(s)=\frac{1}{G(s)}$$

There will be negligible frequency peaking.