Even and Odd Mode Analysis

Analysis in this section will derive S parameters directly.

Wilkinson Power Divider

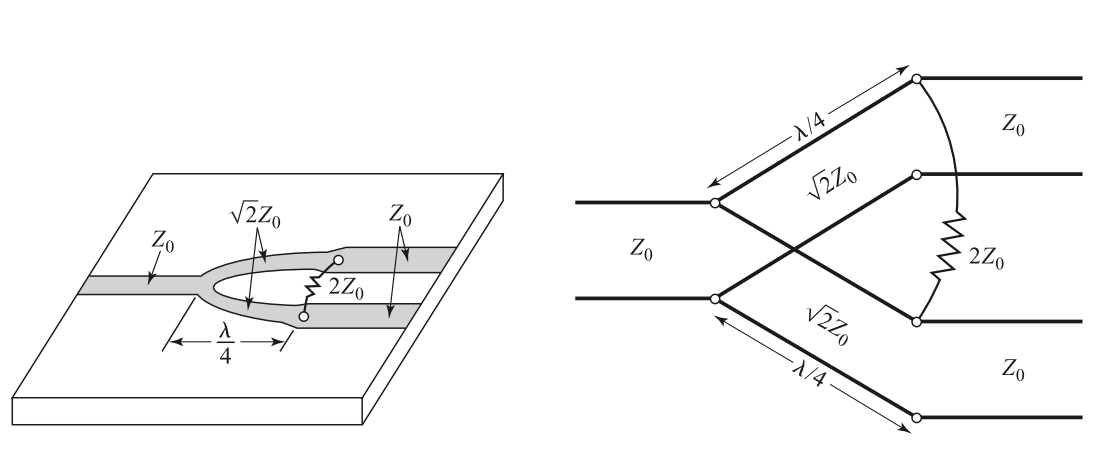
It can be normalized as

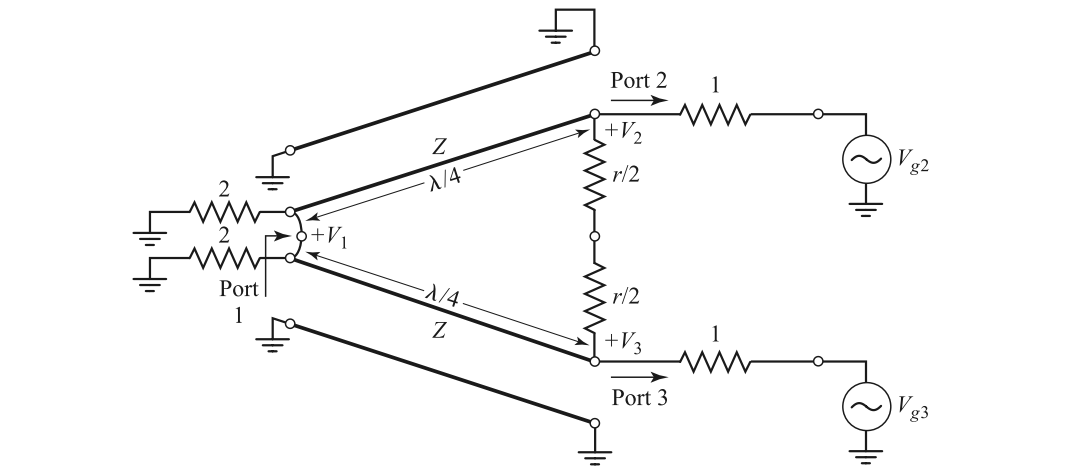
It is assumed that for even mode $V_{g2}=V_{g3}=2V_0$, and for odd mode $V_{g2}=-V_{g3}=2V_0$.

Apply even and odd mode analysis, where $Z=\sqrt{2},r=2$

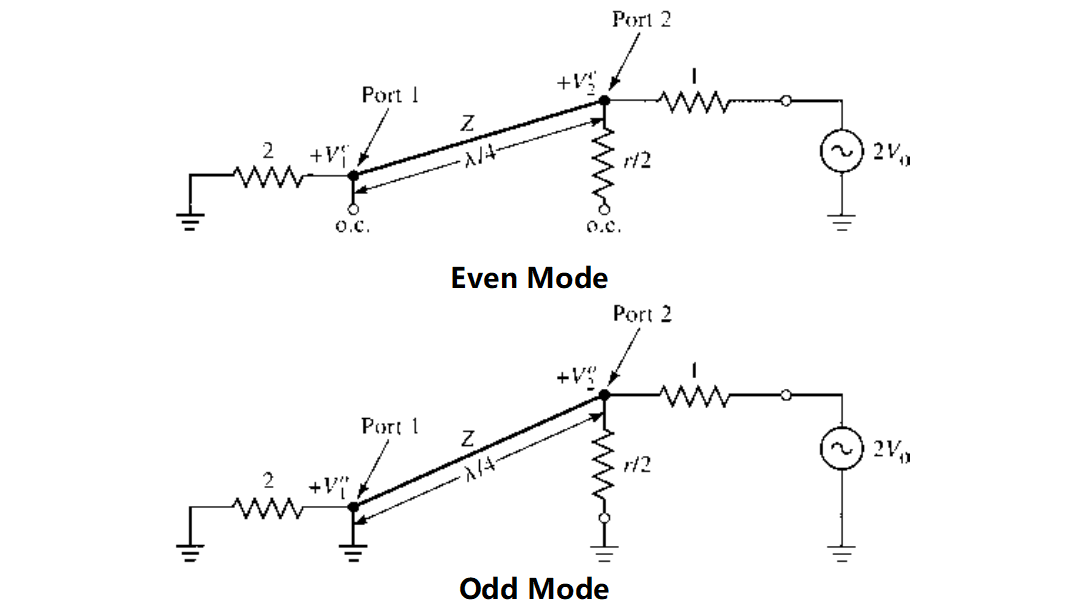
For the even mode, the node 2 is matched, so $V_{2}^e=V_0$. By establishing transmission line equation, we have

$$\begin{aligned} V_1^e&=V(-\lambda/4)=jV^+(1-\Gamma)=V_0\\ V_2^e&=V(0)=V^+(1+\Gamma)=jV_0\frac{\Gamma+1}{\Gamma-1}\\ \Gamma&=\frac{2-\sqrt{2}}{2+\sqrt{2}}\\ V_1^e&=-jV_0\sqrt{2} \end{aligned}$$

For the odd mode, the impedance seen to the left of the port 2 is 1, and the power is dissipated at the resistor. We have $V_1^o=0,V_2^o=V_0$.

$$\begin{aligned} S_{11}&=0 &&Z_{in}=1\\ S_{22}&=S_{33}=0 &&\text{ports 2-3 matched}\\ S_{12}&=S_{21}=\frac{V_1^e+V_1^o}{V_2^e+V_2^o}=-j/\sqrt{2} &&\text{symmetry due to reciprocity}\\ S_{13}&=S_{13}=-j/\sqrt{2} &&\text{symmetry of port 2-3}\\ S_{23}&=S_{32}=0 &&\text{short or open at bisection}\\ \end{aligned}$$

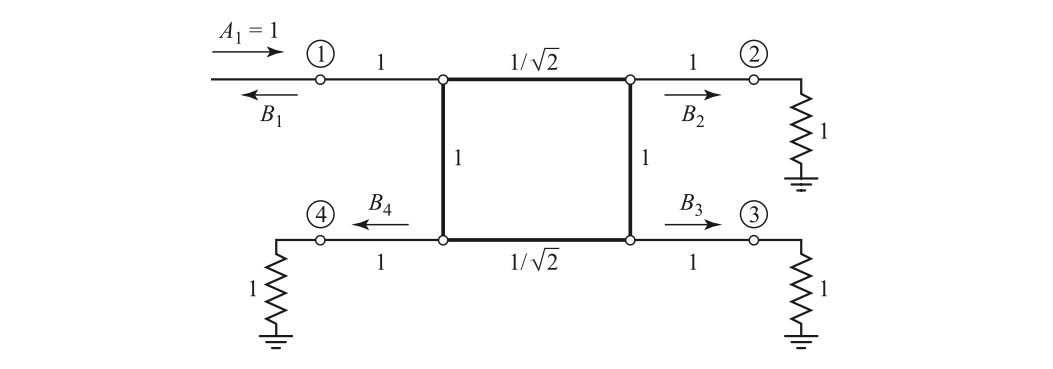
Quadrature (90◦) Hybrid

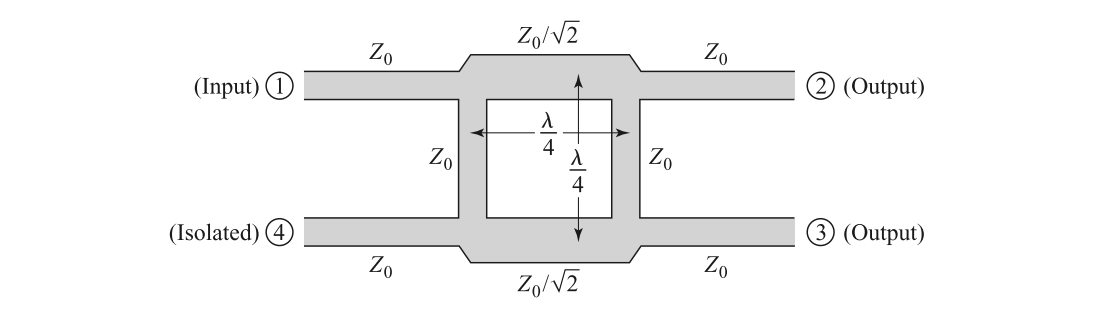
S parameter is

$$\mathbf{S}=\frac{-1}{\sqrt{2}}\left[ \begin{matrix} {0} & {j} & {1} & {0} \\ {j} & {0} & {0} & {1} \\ {1} & {0} & {0} & {j} \\ {0} & {1} & {j} & {0} \end{matrix} \right]$$

Calculation is detailed as follows. It can be normalized as

Apply even and odd mode analysis

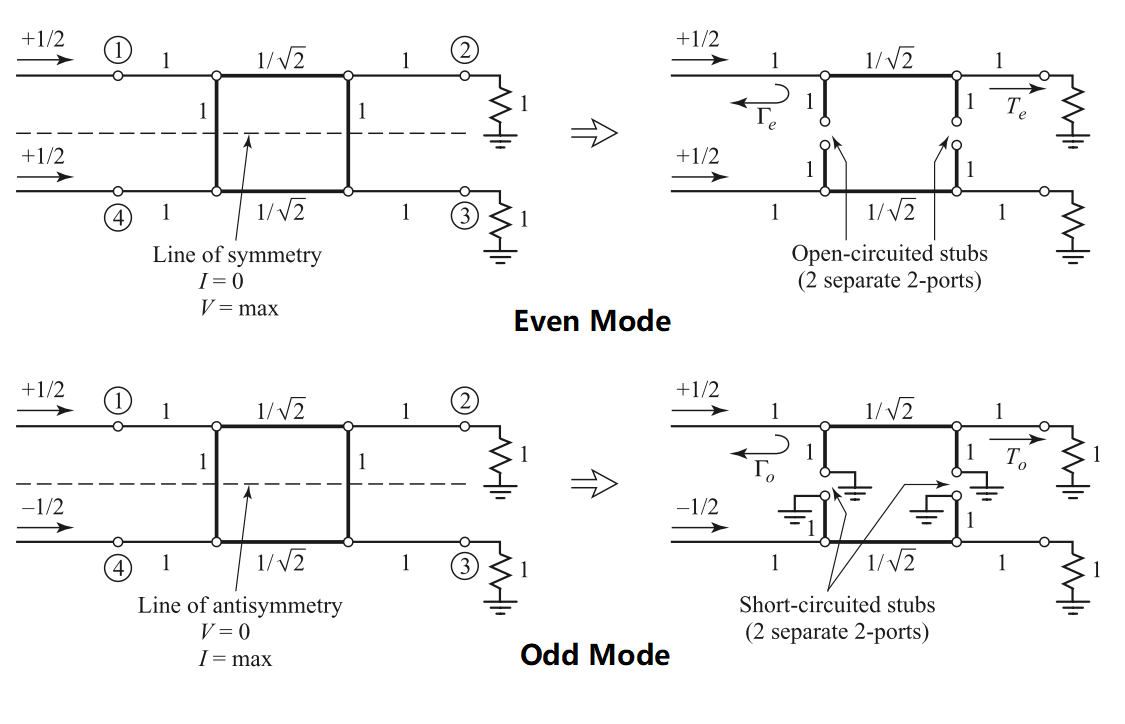
For the even mode, we have

$$\left[ \begin{matrix} A & B \\ C & D \end{matrix} \right]_e= \left[ \begin{matrix} 1 & 0 \\ j & 1 \end{matrix} \right] \left[ \begin{matrix} 0 & j/\sqrt{2} \\ j\sqrt{2} & 0 \end{matrix} \right] \left[ \begin{matrix} 1 & 0 \\ j & 1 \end{matrix} \right]= \frac{1}{\sqrt{2}} \left[ \begin{matrix} -1 & j \\ j & -1 \end{matrix} \right]$$

and thus

$$\begin{aligned} \Gamma_e&=\frac{A+B-C-D}{A+B+C+D}=0\\ T_e&=\frac{2}{A+B+C+D}=\frac{1}{\sqrt{2}}(-1-j) \end{aligned}$$

For the odd mode, we have

$$\left[\begin{matrix}A & B \\C & D\end{matrix}\right]_o=\left[\begin{matrix}1 & 0 \\-j & 1\end{matrix}\right]\left[\begin{matrix}0 & j/\sqrt{2} \\j\sqrt{2} & 0\end{matrix}\right]\left[\begin{matrix}1 & 0 \\-j & 1\end{matrix}\right]=\frac{1}{\sqrt{2}}\left[\begin{matrix}1 & j \\j & 1\end{matrix}\right]$$

and thus

$$\begin{aligned} \Gamma_o&=\frac{A+B-C-D}{A+B+C+D}=0\\ T_o&=\frac{2}{A+B+C+D}=\frac{1}{\sqrt{2}}(1-j) \end{aligned}$$

Suppose a unit wave of $A_1=1$ presents at port 1, it can be decomposed as $A_o=1/2, A_e=1/2$, and thus

$$\begin{aligned} B_1&=\frac{1}{2}\Gamma_e+\frac{1}{2}\Gamma_o=0\\ B_2&=\frac{1}{2}T_e+\frac{1}{2}T_o=-\frac{j}{\sqrt{2}}\\ B_3&=\frac{1}{2}T_e-\frac{1}{2}T_o=-\frac{1}{\sqrt{2}}\\ B_4&=\frac{1}{2}\Gamma_e-\frac{1}{2}\Gamma_o=0 \end{aligned}$$

Other ports can be calculated similarly.

Coupled Line Coupler

$$\mathbf{S}=\left[ \begin{matrix} {0} & {-j\sqrt{1-C^2}} & {C} & {0} \\ {-j\sqrt{1-C^2}} & {0} & {0} & {C} \\ {C} & {0} & {0} & {-j\sqrt{1-C^2}} \\ {0} & {C} & {-j\sqrt{1-C^2}} & {0} \end{matrix} \right]$$

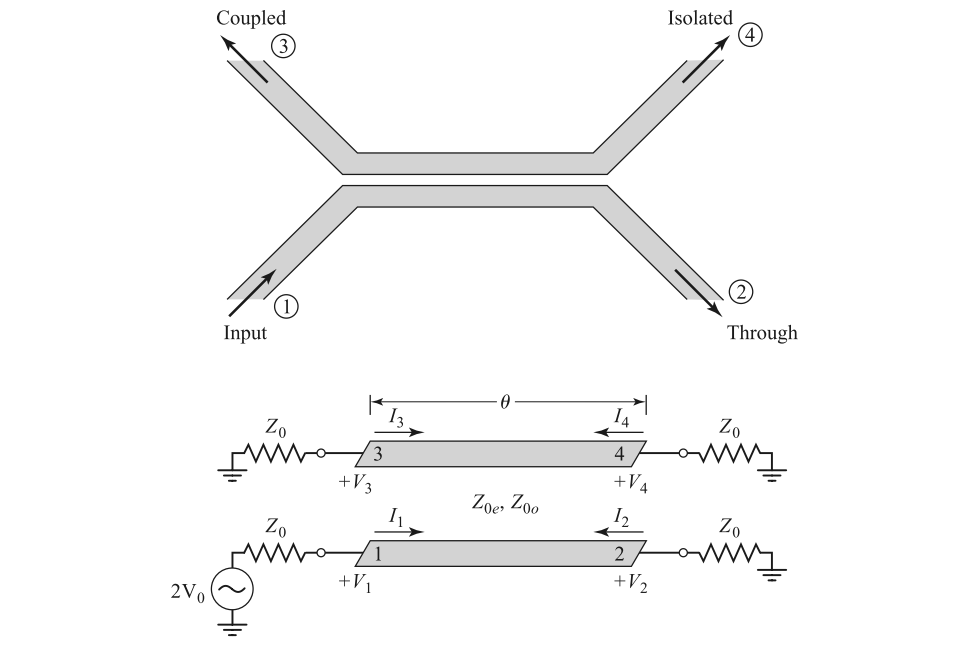
Its equivalent even-odd mode circuit is

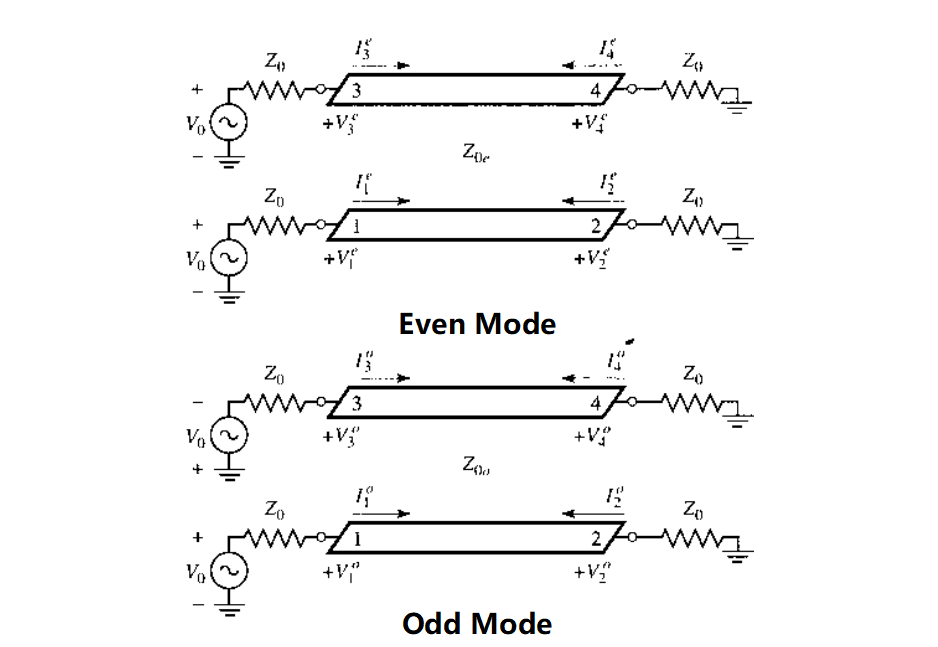
It can be observed that

$$\begin{aligned}V_1^o &= V_0\frac{Z_{in}^o}{Z_{in}^o+Z_0}\\V_1^e &= V_0\frac{Z_{in}^e}{Z_{in}^e+Z_0}\\I_1^o &= \frac{V_0}{Z_{in}^o+Z_0}\\I_1^e &= \frac{V_0}{Z_{in}^e+Z_0}\\Z_{in} &= \frac{V_1^o+V_1^e}{I_1^o+I_1^e}\\ &= Z_0+\frac{2(Z_{in}^oZ_{in}^e-Z_0^2)}{Z_{in}^o+Z_{in}^e+2Z_0}\end{aligned}$$

If we further assume that $Z_0=\sqrt{Z_{0o}Z_{0e}}$, the input impedance is

$$\begin{aligned}Z_{in}^o &= Z_{0o}\frac{Z_0+jZ_{0o}\tan\theta}{Z_{0o}+jZ_0\tan\theta}\\ &=Z_{0o}\frac{\sqrt{Z_{0e}}+j\sqrt{Z_{0o}}\tan\theta}{\sqrt{Z_{0o}}+j\sqrt{Z_{0e}}\tan\theta}\\Z_{in}^e &= Z_{0e}\frac{Z_0+jZ_{0e}\tan\theta}{Z_{0e}+jZ_0\tan\theta}\\ &=Z_{0e}\frac{\sqrt{Z_{0o}}+j\sqrt{Z_{0e}}\tan\theta}{\sqrt{Z_{0e}}+j\sqrt{Z_{0o}}\tan\theta}\\\end{aligned}$$

It follows that $Z_{in}^eZ_{in}^o=Z_{0e}Z_{0o}=Z_0^2$, and $Z_{in}=Z_0$. Hence, all ports will be matched. Voltage at the ports can be written as

$$\begin{aligned}V_3 &=V_1^e-V_1^o\\&= V_0\frac{j(Z_{0e}-Z_{0o})\tan{\theta}}{2Z_0+j(Z_{0e}+Z_{0o})\tan{\theta}}\\\end{aligned}$$

Assume that

$$C=\frac{Z_{0e}-Z_{0o}}{Z_{0e}+Z_{0o}}$$

Several inferences are

$$\sqrt{1-C^2}=2Z_0/(Z_{0e}+Z_{0o})\\ Z_{0e}=Z_0\sqrt{\frac{1+C}{1-C}}\\ Z_{0o}=Z_0\sqrt{\frac{1-C}{1+C}}$$

With these annotation, we may rewrite $V_3$ as

$$V_3=V_0\frac{jC\tan\theta}{\sqrt{1-C^2}+j\tan\theta}$$

$V_2, V_4$ are derived as follow.

$$\Gamma_e=\frac{Z_0-Z_{0e}}{Z_0+Z_{0e}}\\ \Gamma_o=\frac{Z_0-Z_{0o}}{Z_0+Z_{0o}}\\ V_2^e=V_1^e\frac{1+\Gamma_e}{e^{j\theta}+\Gamma_e e^{-j\theta}}\\ V_2^o=V_1^e\frac{1+\Gamma_o}{e^{j\theta}+\Gamma_o e^{-j\theta}}$$

Those equations lead to

$$V_2=V_2^e+V_2^o=V_0\frac{\sqrt{1-C^2}}{\sqrt{1-C^2}\cos\theta+j\sin\theta}\\ V_4=V_2^e-V_2^o=0$$

These results can be used to derive the S parameter. If the electrical length is $\pi/4$, we may write the S parameter as in the beginning.

Termination

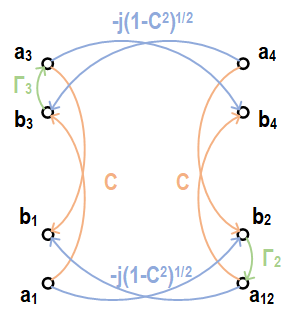
Thus, we may write

$$\begin{aligned} S_{11,new} &= S_{21}S_{12}\Gamma_2+S_{31}S_{13}\Gamma_3\\ &=C^2\Gamma_3-(1-C^2)\Gamma_2\\ S_{41,new} &= S_{42}S_{21}\Gamma_2+S_{43}S_{31}\Gamma_3\\ &=-jC\sqrt{1-C^2}(\Gamma_2+\Gamma_3) \end{aligned}$$

In the case that $C=\sqrt{2}/2, \Gamma_3=-\Gamma_2=1$, we have $S_{11,new}=1,S_{41,new}=0$. Thus, it constitute an all-stop filter, as having been derived using the network parameters. In the case that $C=\sqrt{2}/2,\Gamma_3=\Gamma_2=\Gamma$, we have $S_{11,new}=0,S_{41,new}=-j\Gamma$. This is the result that leads to the design of reflective-type attenuator and reflective-type phase shifter. Note that $\Gamma$ is defined as

$$\Gamma=\frac{Z_L-Z_0}{Z_L+Z_0}$$

Marchand Balun

General Balun

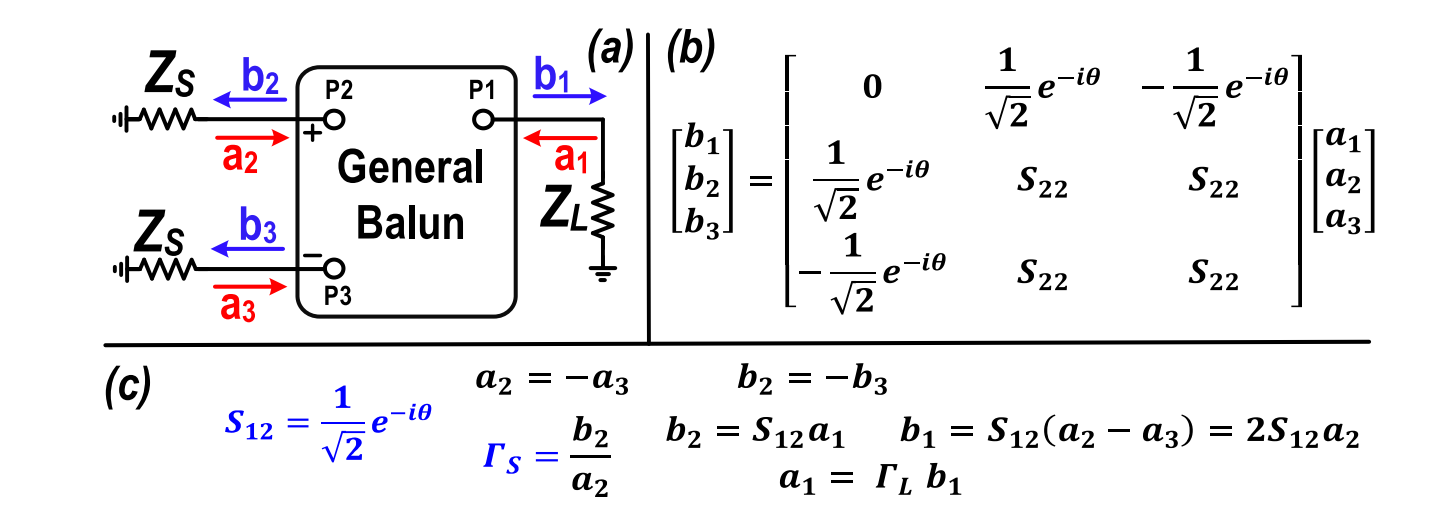
It is assumed that the general balun has the following properties:

• Single-ended port is matched ($S_{11}=0$).
• Differential ports are matched ($S_{22}=S_{23}=S_{32}=S_{33}$).
• The power present at the common port is evenly divided between the two differential ports with opposite polarity ($S_{21}=(1/\sqrt{2})e^{-j\theta},S_{31}=-(1/\sqrt{2})e^{-j\theta}$).

To illustrate the second point, the following schematic is adopted.

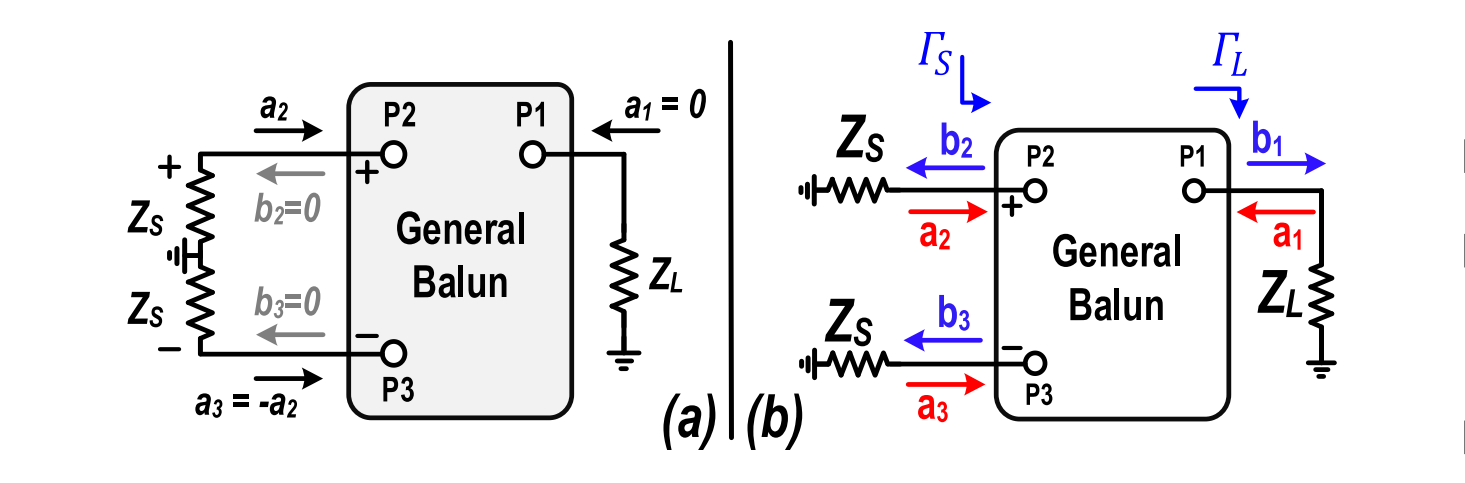
For differential excitation at the left side, we have $a_2=-a_3, b_2=b_3=0$. It follows that

$$0=b_2=S_{21}a_1+S_{22}a_2+S_{23}a_3=(S_{22}-S_{23})a_2$$

The relation between the source and the load reflection coefficients are

$$\Gamma_S=\frac{b_2}{a_2}=\frac{S_{12}a_1}{b_1/2S_{12}}=\Gamma_Le^{-2j\theta}$$

If $\theta=0/\pi$, we have $Z_S=(Z_{S0}/Z_{L0})Z_L$, which features an impedance scaling balun; if $\theta=\pm\pi/2$, we have $Z_S=(Z_{L0}/Z_{S0})(1/Z_L)$, which demonstrates an impedance inverting balun.

Requirement of Balun

A variety of three-port balun, when adding an “invisible port 4,” are inherently symmetrical structures. The following structure is considered for analysis.

When the differential and common excitation is applied.

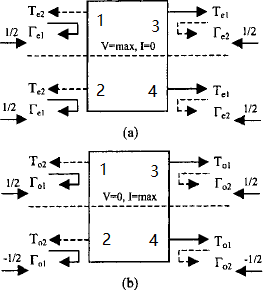
The mixed-mode S parameter can be obtained as

$$\mathbf{S^{mm}}= \left[ \begin{matrix} {\Gamma_{o1}} & {T_{o2}} & {0} & {0} \\ {T_{o1}} & {\Gamma_{o2}} & {0} & {0} \\ {0} & {0} & {\Gamma_{e1}} & {T_{e2}} \\ {0} & {0} & {T_{e1}} & {\Gamma_{e2}} \end{matrix} \right]$$

It can be converted to the standard S parameter as

$$\mathbf{S^{std}}=\frac{1}{2} \left[ \begin{matrix} {\Gamma_{e1}+\Gamma_{o1}} & {\Gamma_{e1}-\Gamma_{o1}} & {T_{e2}+T_{o2}} & {T_{e2}-T_{o2}} \\ {\Gamma_{e1}-\Gamma_{o1}} & {\Gamma_{e1}+\Gamma_{o1}} & {T_{e2}-T_{o2}} & {T_{e2}+T_{o2}} \\ {T_{e2}+T_{o2}} & {T_{e2}-T_{o2}} & {\Gamma_{e2}+\Gamma_{o2}} & {\Gamma_{e2}-\Gamma_{o2}} \\ {T_{e2}-T_{o2}} & {T_{e2}+T_{o2}} & {\Gamma_{e2}-\Gamma_{o2}} & {\Gamma_{e2}+\Gamma_{o2}} \end{matrix} \right]$$

Using Mason's formula, the 3-port S parameter with port 2 terminated with $\Gamma$ is

$$S_{21,new}=S_{31}+\frac{S_{32} S_{21} \Gamma}{1-S_{22}\Gamma}\\ S_{31,new}=S_{41}+\frac{S_{42} S_{21} \Gamma}{1-S_{22}\Gamma}$$

It must satisfy

$$S_{21, new}=-S_{31, new}\\ S_{11,new}=0$$

which lead us to

$$\frac{T_{e1}(1-\Gamma_{o1}\Gamma)}{2-\Gamma(\Gamma_{e1}+\Gamma_{o1})}=0\\ \frac{\Gamma_{e1}+\Gamma_{o1}-2\Gamma_{e1}\Gamma_{o1}\Gamma}{2-\Gamma(\Gamma_{e1}+\Gamma_{o1})} = 0$$

Using the following even and odd mode definition, we have

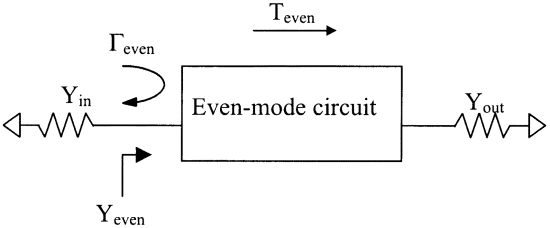
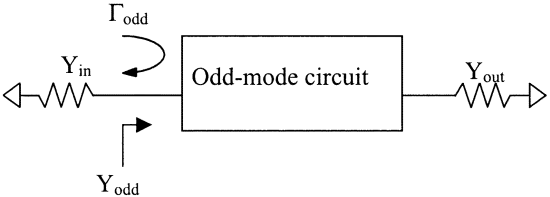
The reflection coefficient is

$$\Gamma_{e1}=\frac{Z_e-Z_{in}}{Z_e+Z_{in}}=\frac{Y_{in}-Y_e}{Y_{in}+Y_e}\\ \Gamma_{o1}=\frac{Z_o-Z_{in}}{Z_o+Z_{in}}=\frac{Y_{in}-Y_o}{Y_{in}+Y_o}$$

It can be used to solve for the requirement of balun, as

$$\begin{aligned} T_{even}=0&\\ Y_{even}+Y_{odd}=2Y_{in}&,\ \Gamma=-1\quad(\mathrm{short})\\ \frac{1}{Y_{even}}+\frac{1}{Y_{odd}}=\frac{2}{Y_{in}}&,\ \Gamma=1\quad(\mathrm{open}) \end{aligned}$$

Marchand Balun Formulation

To prove that Marchand balun is indeed a balun

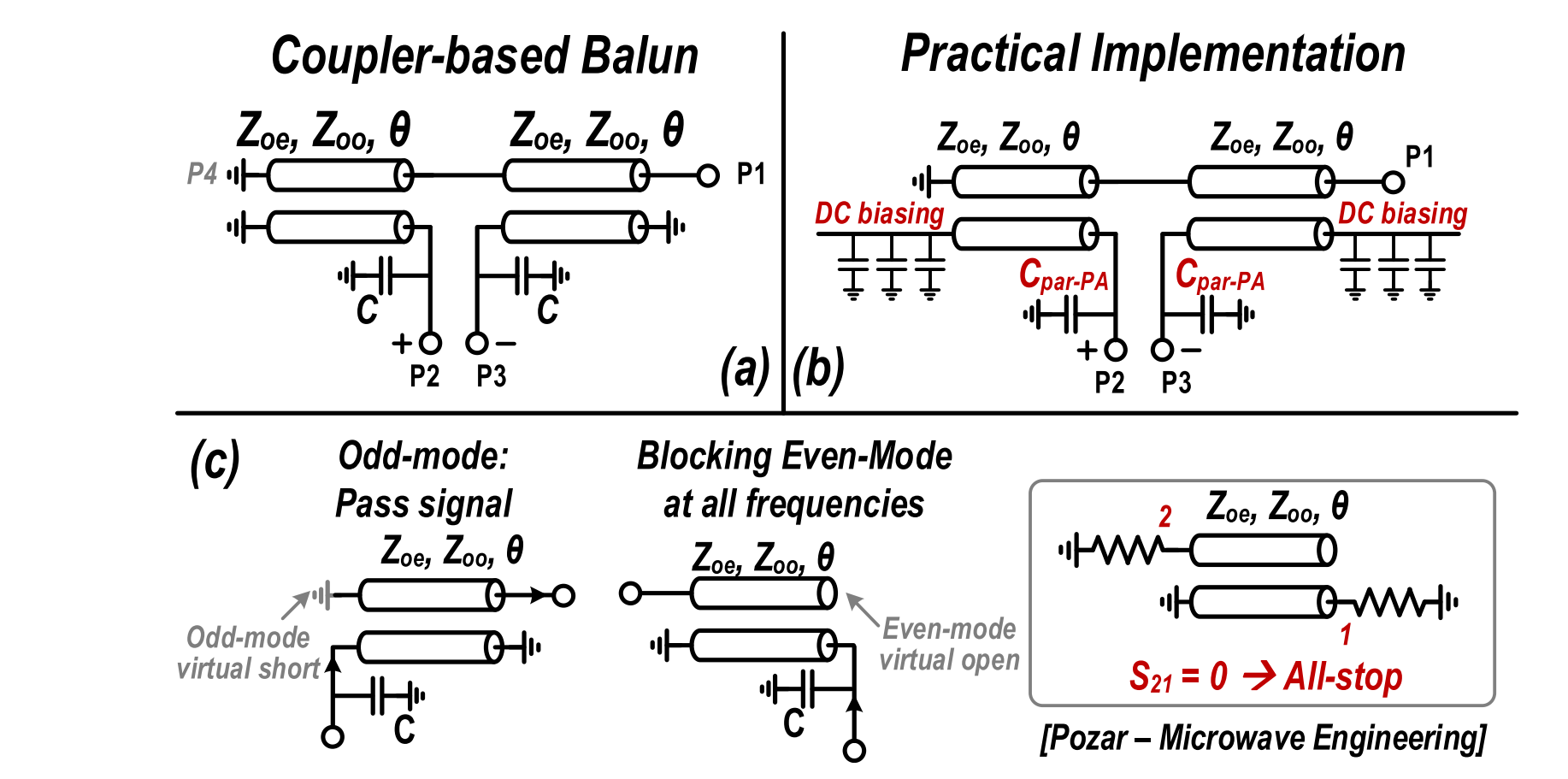
we need to add a virtual port to facilitate decomposing into even-mode and odd-mode circuits. Note that for the even-mode circuit, the coupled line with short and open termination features an all-stop filter, so that the requirement $T_e=0$ is indeed satisfied.

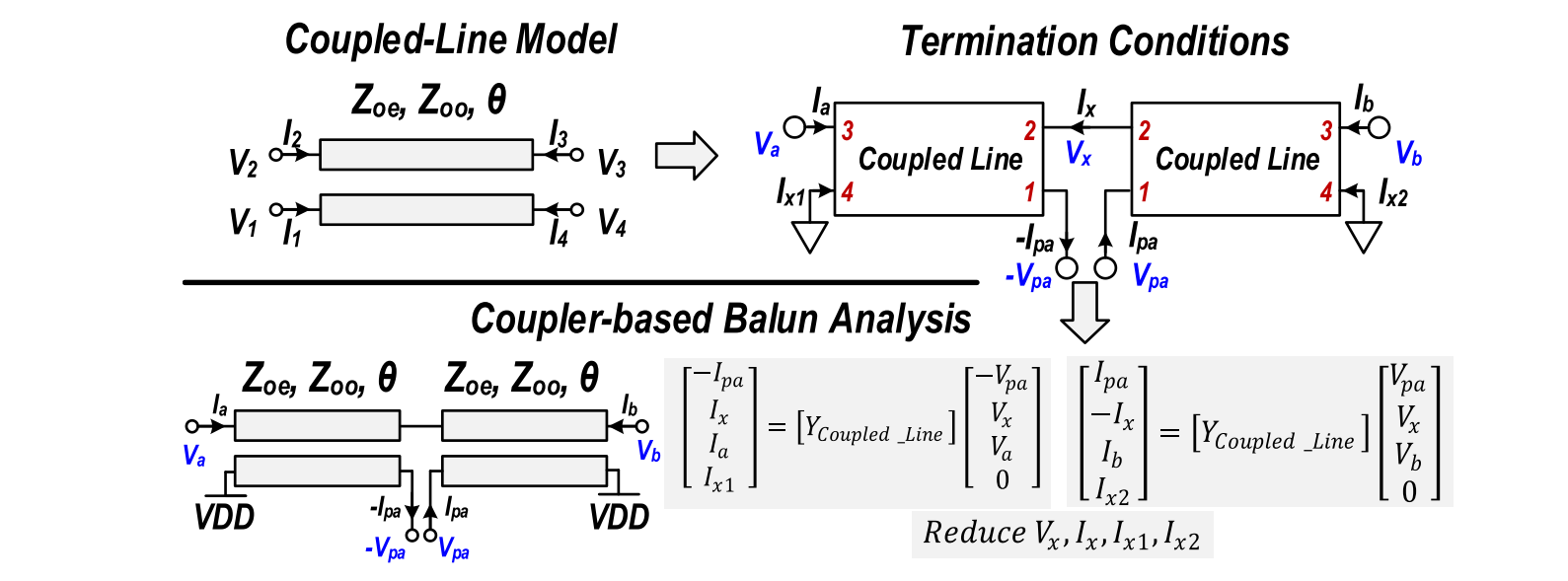
which leads to

$$\left[ \begin{matrix} I_{pa}\\ I_a\\ I_b \end{matrix} \right] = \left[ \begin{matrix} {-jY_p\cot(\theta)} & {jY_m\csc(\theta)/2} & {-jY_m\csc(\theta)/2} \\ {jY_m\csc(\theta)} & {-jY_p\cot(2\theta)} & {jY_p\csc(2\theta)} \\ {-jY_m\csc(\theta)} & {jY_p\csc(2\theta)} & {-jY_p\cot(2\theta)} \end{matrix} \right] \left[ \begin{matrix} V_{pa}\\ V_a\\ V_b \end{matrix} \right]$$

where $Y_p=(Y_{0o}+Y_{0e})/2,Y_m=(Y_{0o}-Y_{0e})/2, Y_{0e}=1/Z_{0e}, Y_{0o}=1/Z_{0o}$.

Since $V_b=0$, the third row and the third column can be eliminated. It follows that

$$\left[ \begin{matrix} I_{pa}\\ I_L\\ \end{matrix} \right] = \left[ \begin{matrix} {-jY_p\cot(\theta)} & {jY_m\csc(\theta)/2} \\ {jY_m\csc(\theta)} & {-jY_p\cot(2\theta)} \end{matrix} \right] \left[ \begin{matrix} V_{pa}\\ V_L\\ \end{matrix} \right]$$

Impedance Inverting Balun

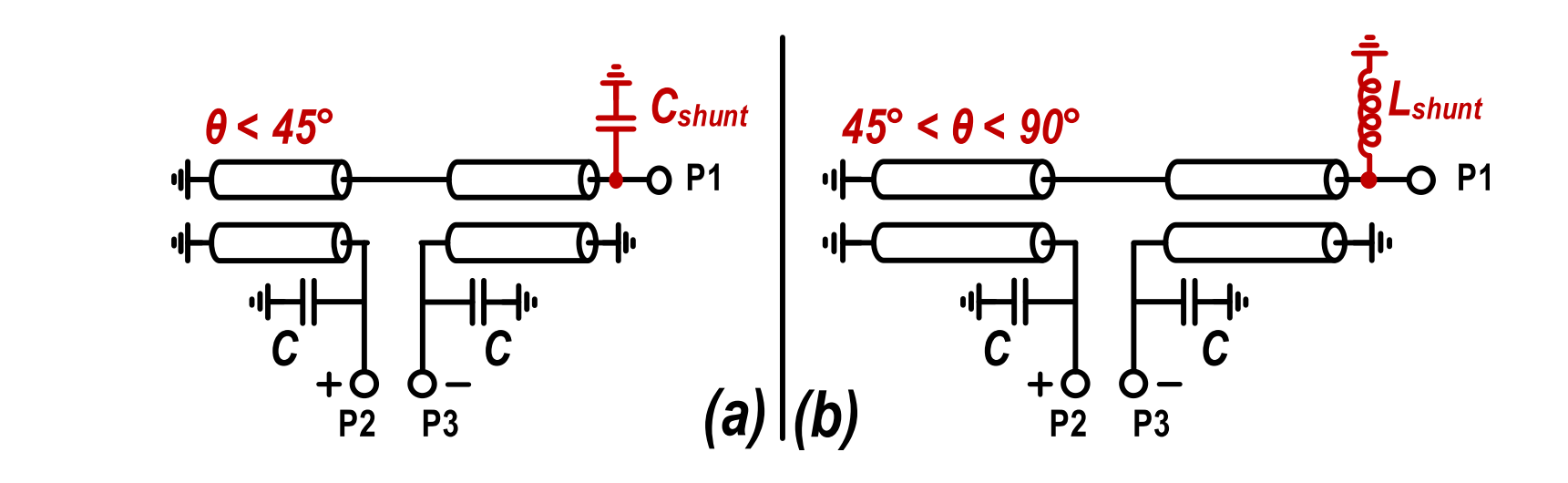
A capacitor is therefore required to resonate out the parasitic inductance. At the PA side, a capacitor is required as

$$Y_C=jY_p\cos(\theta)$$

which can absorb the parasitic capacitance of the PA output. As for the reactance at the load side

$$Y_{C_{Shunt}/L_{Shunt}}=jY_p\cos(2\theta)$$

In that case, the input impedance is

$$\left[ \begin{matrix} I_{pa}\\ I_L\\ \end{matrix} \right] = \left[ \begin{matrix} {0} & {jY_m\csc(\theta)/2} \\ {jY_m\csc(\theta)} & {0} \end{matrix} \right] \left[ \begin{matrix} V_{pa}\\ V_L\\ \end{matrix} \right]$$

and the input impedance is

$$Z_{pa}=\frac{1}{Z_L}\left(\frac{\sqrt{2}}{Y_m\csc(\theta)}\right)^2$$

Appendix

Mathematica derivation of Y parameter of the Marchand balun

(* This is the Y parameter of the coupled transmission line *)
Y = {{-I Yp Cot[t], I Ym Cot[t], -I Ym Csc[t], 
    I Yp Csc[t]}, {I Ym Cot[t], -I Yp Cot[t], 
    I Yp Csc[t], -I Ym Csc[t]}, {-I Ym Csc[t], 
    I Yp Csc[t], -I Yp Cot[t], 
    I Ym Cot[t]}, {I Yp Csc[t], -I Ym Csc[t], 
    I Ym Cot[t], -I Yp Cot[t]}};
(* Set boundary conditions *)
y1 = {{-Ipa}, {Ix}, {Ia}, {Ix1}};
x1 = {{-Vpa}, {Vx}, {Va}, {0}};
y2 = {{Ipa}, {-Ix}, {Ib}, {Ix2}};
x2 = {{Vpa}, {Vx}, {Vb}, {0}};
(* Eliminate unnecessary variables *)
R = Eliminate[{y1 == Y.x1, y2 == Y.x2}, {Vx, Ix, Ix1, Ix2}];
Solve[R, {Ipa, Ia, Ib}]

Proof of the requirement of the balun

(* Conversion to the standard S parameter *)
M = 1/Sqrt[2] ({
     {1, -1, 0, 0},
     {0, 0, 1, -1},
     {1, 1, 0, 0},
     {0, 0, 1, 1}
    });
Smm = ({
    {Go1, To2, 0, 0},
    {To1, Go2, 0, 0},
    {0, 0, Ge1, Te2},
    {0, 0, Te1, Ge2}
   });
Snew = Simplify[Inverse[M].Smm.M];
(* Apply boundary conditions, and use Mason's formula to simplify it as 3-port S parameter *)
S11 = Snew[[1, 1]] + Snew[[1, 2]] Snew[[2, 1]] G/(1 - G Snew[[2, 2]]);
S21 = Snew[[3, 1]] + Snew[[3, 2]] Snew[[2, 1]] G/(1 - G Snew[[2, 2]]);
S31 = Snew[[4, 1]] + Snew[[4, 2]] Snew[[2, 1]] G/(1 - G Snew[[2, 2]]);
(* Solve for the equivalent requirement of the balun *)
R1 = Together[S21 + S31];
R2 = Together[S11];
rule = {Ge1 -> (Yin - Ye)/(Yin + Ye), Go1 -> (Yin - Yo)/(Yin + Yo)};
Reduce[(R1 /. rule) == 0 && (R2 /. rule) == 0]

Reference

For the derivation of coupled transmission line, Wilkinson power divider, quadrature hybrid, and coupled line coupled, refer to

• D. M. Pozar, Microwave Engineering. NJ, Hoboken: Wiley, 1998.

For the theoretical analysis of balun, refer to

• K. S. Ang, Y. C. Leong and C. H. Lee, "Analysis and design of miniaturized lumped-distributed impedance-transforming baluns," IEEE Trans. Microw. Theory Techn., vol. 51, no. 3, pp. 1009-1017, March 2003, doi: 10.1109/TMTT.2003.808677.
• Y. C. Leong, K. S. Ang and C. H. Lee, "A derivation of a class of 3-port baluns from symmetrical 4-port networks," 2002 IEEE MTT-S Int. Microw. Symp. Digest, Seattle, WA, USA, 2002, pp. 1165-1168 vol.2, doi: 10.1109/MWSYM.2002.1011855.

For the insightful analysis of coupled line balun, refer to

• H. T. Nguyen and H. Wang, "A coupler-based differential mm-wave Doherty power amplifier with impedance inverting and scaling baluns," IEEE J. Solid-State Circuits, doi: 10.1109/JSSC.2020.2970708.