二阶系统 | Triblemany

从汽车的悬挂系统到电路中的滤波器，二阶系统无处不在。它们是理解现实世界动态行为的基石。本文将深入探讨二阶系统的核心概念，分析其瞬态和稳态响应，帮助你建立一个清晰而完整的知识框架。

什么是二阶系统？

在控制理论和信号处理中，如果一个系统的行为可以用一个二阶常微分方程来描述，那么它就是一个二阶系统。其标准形式的传递函数为：

$G(s)=\frac{\omega_n^2}{s^2+2\zeta\omega_ns+\omega_n^2}$

这个简单的公式由两个核心参数主导系统的全部特性：

自然频率 $\omega_n$ (Natural Frequency): 想象一个没有摩擦或空气阻力的秋千，它会以一个固定的频率来回摆动，这就是它的自然频率。在二阶系统中，$\omega_n$ 代表了系统在无阻尼情况下的固有振荡频率。
阻尼比 $\zeta$ (Damping Ratio): 这个无量纲参数描述了系统振荡衰减的快慢。$\zeta=0$ 意味着没有阻尼（像那个理想秋千），而$\zeta$越大，振荡消失得越快。

将$s=j\omega$代入，我们可以得到系统的频率响应表达式：

$G(j\omega)=\frac{1}{1-(\frac{\omega}{\omega_n})^2+j2\zeta\frac{\omega}{\omega_n}}$

在电子学中，我们常用品质因数Q (Quality Factor)来描述谐振电路的特性，它与阻尼比的关系为 $Q=1/(2\zeta)$。高Q值意味着低阻尼和更强的谐振。

瞬态分析：系统如何响应突变？

瞬态分析关注的是系统在受到一个突发输入（如阶跃信号）后的即时反应。系统的行为完全由其极点决定。通过求解特征方程 $s^2+2\zeta\omega_ns+\omega_n^2=0$，我们得到极点：

$p_{1,2} = -\zeta\omega_n \pm \omega_n\sqrt{\zeta^2-1}$

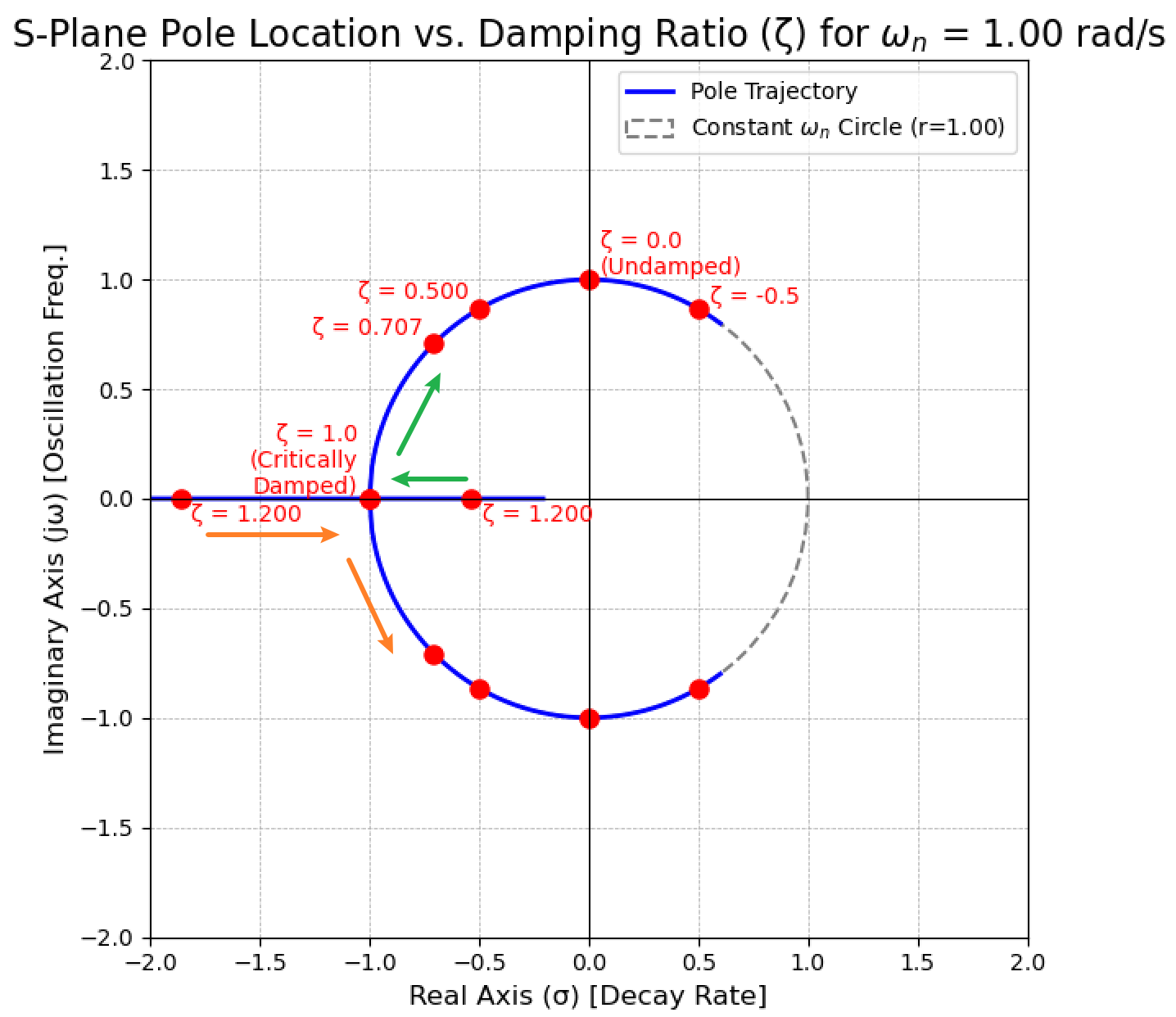
极点的位置随着阻尼比$\zeta$的变化而变化，从而根本上改变了系统的行为。其实部定义为阻尼（damping）:

$\sigma=-\zeta\omega_n$

虚部定义为衰减后振荡频率（damped natural frequency）:

$\omega_d=\omega_n\sqrt{1-\zeta^2}$

根据$\zeta$的取值，系统的响应可以分为以下几种情况：

$\zeta<-1$，极点为右半平面一对不相等实数（无震荡发散）
$\zeta=-1$，极点为右半平面一对相等实数（发散，无震荡临界情况）
$-1<\zeta<0$，极点为右半平面一对复数（震荡发散）
$\zeta=0$，极点为虚轴上一对大小相等符号相反的虚数（无衰减震荡）
$0<\zeta<1$，极点为左半平面一对复数（欠阻尼衰减）
$\zeta=1$，极点为左半平面一对相等实数（衰减，临界阻尼）
$\zeta>1$，极点为左半平面一对不相等实数（过阻尼衰减）

阶跃响应分析

当有输入信号为阶跃函数时，有

$\begin{aligned} Y(s) &=G(s) \cdot U(s) \\ &=\frac{\omega_{n}^{2}}{s^{2}+2 \zeta \omega_{n} s+\omega_{n}^{2}} \cdot \frac{1}{s} \\ &=\frac{\omega_{n}^{2}}{(s+\sigma)^{2}+\omega_{d}^{2}} \cdot \frac{1}{s} \\ &=\frac{1}{s}-\frac{s+\sigma}{(s+\sigma)^{2}+\omega_{d}^{2}}-\frac{\sigma}{\omega_{d}} \frac{\omega_{d}}{(s+\sigma)^{2}+\omega_{d}^{2}} \end{aligned}$

相应的时域表达式为

$\begin{aligned} y(t) &=1-e^{-\sigma t} \cos \omega_{d} t-\frac{\sigma}{\omega_{d}} e^{-\sigma t} \sin \omega_{d} t \\ &=1-e^{-\sigma t}\left(\cos \omega_{d} t+\frac{\sigma}{\omega_{d}} \sin \omega_{d} t\right), t \geq 0 \end{aligned}$

对于$\omega_n=2\pi$，不同$\zeta$时阶跃响应如下图

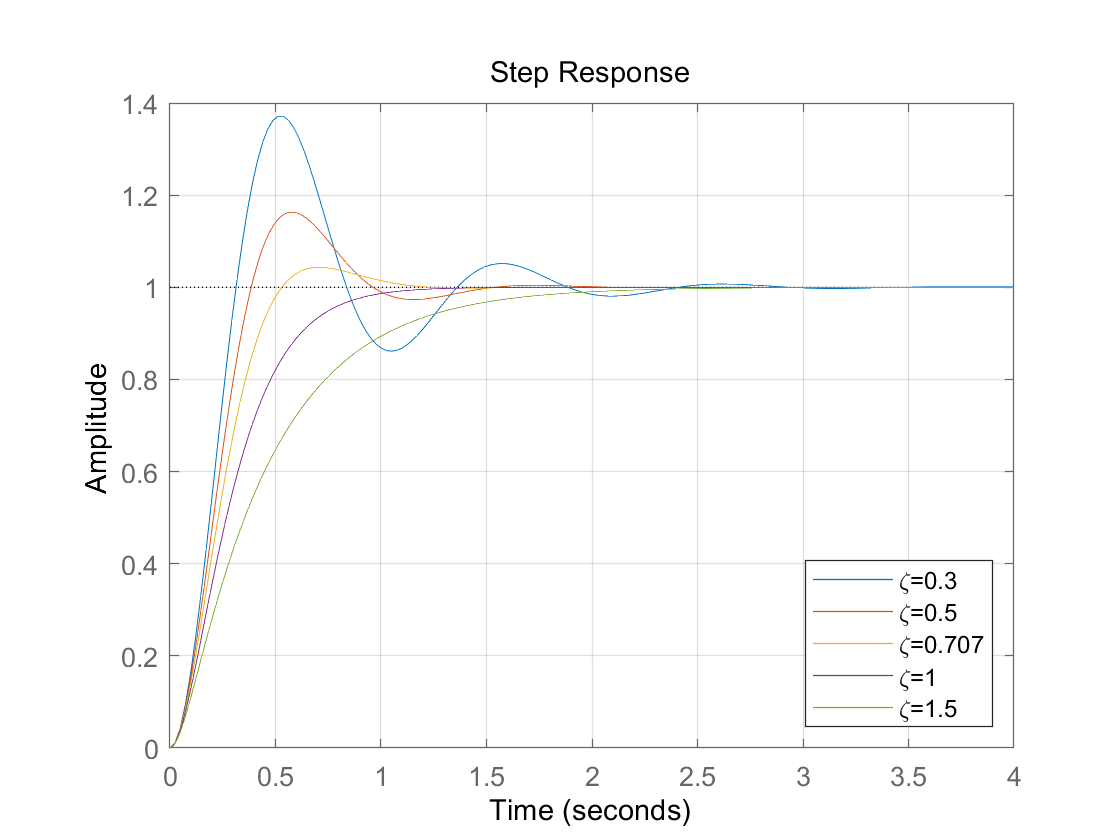
step-response

对于工程应用，我们常用以下指标来量化欠阻尼系统的性能：

峰值时间 ($t_p$): 响应达到第一个峰值所需的时间：$t_p = \frac{\pi}{\omega_d} = \frac{\pi}{\omega_n\sqrt{1-\zeta^2}}$
超调量 (%OS): 响应超过最终值的最大百分比，它只与阻尼比有关：$\%OS = e^{\frac{-\zeta\pi}{\sqrt{1-\zeta^2}}} \times 100\%$
调节时间 ($t_s$): 响应进入并保持在终值$\pm\delta$误差带内所需的时间：$t_s = \frac{\ln(1/\delta)}{\zeta\omega_n}$
- 对于一阶系统，$t_s = \tau\cdot\ln(1/\delta)$

稳态分析：系统如何响应不同频率？

稳态分析（或称频率响应分析）研究的是系统对不同频率正弦输入的响应。

幅频响应为

$A(\omega)=|G(j \omega)|=\frac{1}{\sqrt{\left[1-\left(\frac{\omega}{\omega_{n}}\right)^{2}\right]^{2}+\left(2 \zeta \frac{\omega}{\omega_{n}}\right)^{2}}}$

相频响应为

$\varphi(\omega)=-180^{\circ}+\arctan \frac{\left(\frac{\omega}{\omega_{n}}\right)^{2}-1}{2 \zeta \frac{\omega}{\omega_{n}}}$

分析三种边界情况，有

$\begin{aligned} \omega=0 &\quad A(0)=1, \varphi(0)=0^{\circ} \\ \omega=\omega_{n} &\quad A(\omega)=\frac{1}{2 \zeta},\varphi\left(\omega_{n}\right)=-90^{\circ} \\ \omega \rightarrow \infty &\quad A(\infty)=0, \varphi(\infty)=-180^{\circ} \end{aligned}$

对幅频响应的分母求极值，得到谐振频率:

$\omega_r=\omega_n\sqrt{1-2\zeta^2}$

以及谐振时的幅值和相位

$A(\omega_r)=\frac{1}{2\zeta\sqrt{1-\zeta^2}}$ $\varphi(\omega_r)=-\arctan\frac{\zeta}{\sqrt{1-2\zeta^2}}$

因此，阻尼因子$\zeta $决定了

当$\zeta>1/\sqrt{2}$时，不存在谐振频率
当$\zeta=1/\sqrt{2}$时，$\omega_r=0, A(\omega_r)=1, \varphi(\omega_r)=0$
当$0<\zeta<1/\sqrt{2}$时，存在谐振频率
当$\zeta=0$时，$\omega_r=\omega_n, A(\omega_r)\rightarrow\infty, \varphi(\omega_r)=-90^{\circ}$

同样的，对于$\omega_n=2\pi$，不同$\zeta$时频率响应如下图

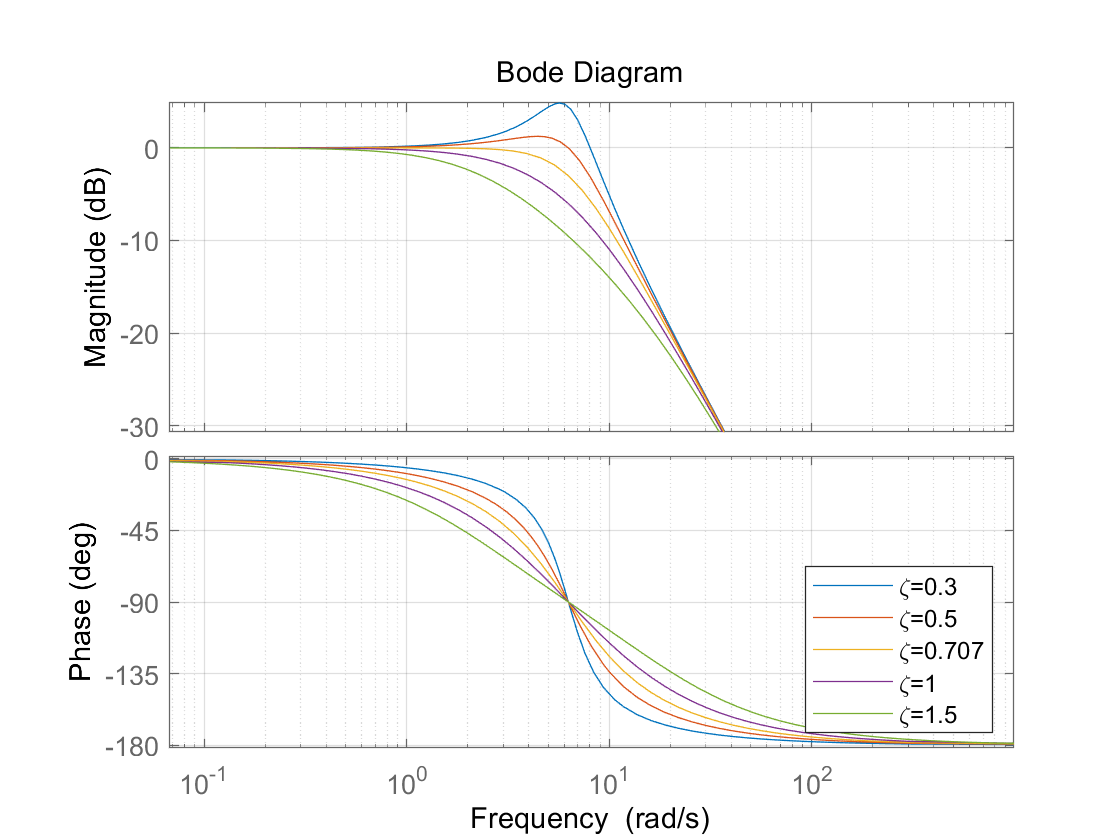
frequency-response

总结

二阶系统的行为完全由其自然频率 $\omega_n$ 和阻尼比 $\zeta$ 共同决定。这两个参数定义了极点在S平面中的位置，从而决定了系统：

瞬态响应的形态（过阻尼、临界阻尼或欠阻尼），包括其响应速度、超调和振荡特性。
频率响应的形态，包括其带宽、是否存在谐振峰以及谐振的剧烈程度。

掌握了二阶系统的分析方法，就掌握了理解从简单电路到复杂机电系统动态特性的钥匙。

参考

控制理论学习笔记（4）——一阶系统和二阶系统.
孙晓波, 李双全, 王海英. 自动控制原理. 科学出版社, 2006.