Coupled Transmission Line and Its Applications

This article will cover

• Calculation of Z and Y parameters of coupled transmission line.
• Different configuration of the coupled transmission line used as two-port network.
• Conversion between the standard S parameter and the mixed-mode S parameter.

Coupled Transmission Line Formulation

The Z parameter of a lossless transmission line is:

$$\mathbf{Z}= \left[ \begin{matrix} -jZ_0\cot\theta & -jZ_0\csc\theta\\ -jZ_0\csc\theta & -jZ_0\cot\theta \\ \end{matrix} \right]$$

where $\theta=\beta l$ and $Z_0$ is the characteristic impedance.

Method 1

The schematic used for analysis is

$$v_a^1(0)=(-jZ_{0e}\cot\theta)i_1\\ v_a^3(0)=(-jZ_{0e}\csc\theta)i_3\\ v_a^2(0)=(-jZ_{0o}\cot\theta)i_2\\ v_a^4(0)=(-jZ_{0o}\csc\theta)i_4\\ V_1=v_a^1(0)+v_a^2(0)+v_a^3(0)+v_a^4(0)$$

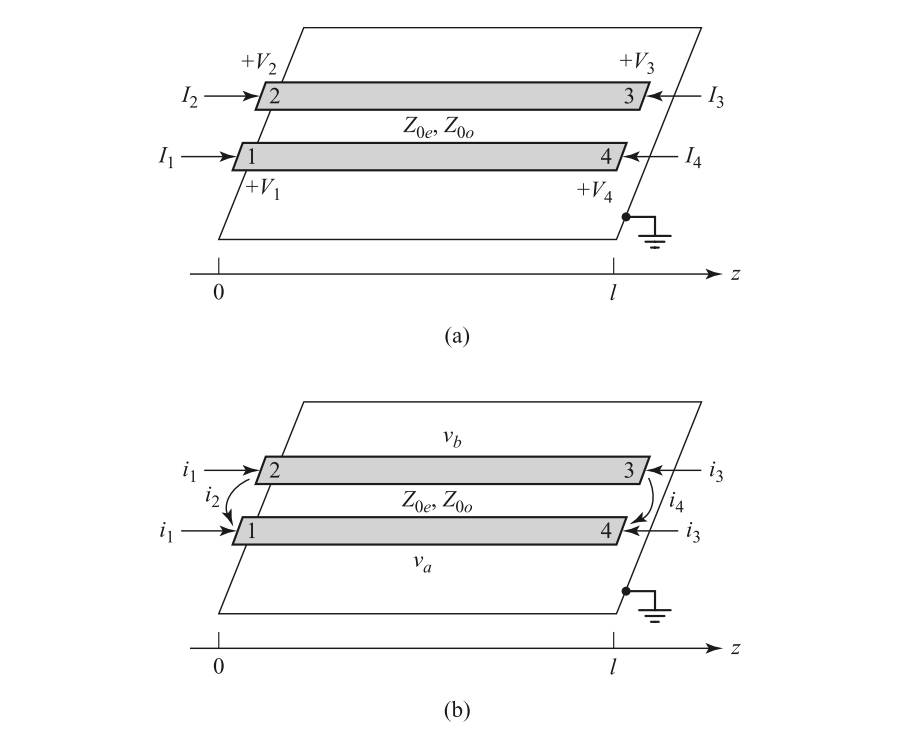
where $v_a^1(0)$ represent the voltage induced by current $i_1$ at position 0 of conductor a. The current relation between the normal and the mixed-mode is:

$$\begin{align} i_1 &= \frac{1}{2} (I_1 + I_2) \\ i_2 &= \frac{1}{2} (I_1 - I_2) \\ i_3 &= \frac{1}{2} (I_3 + I_4) \\ i_4 &= \frac{1}{2} (I_4 - I_3) \end{align}$$

Combine two equations, we have

$$\begin{align} V_1 &= \frac{-j}{2}(Z_{0e}I_1+Z_{0e}I_2+Z_{0o}I_1-Z_{0o}I_2)\cot\theta\\ &= \frac{-j}{2}(Z_{0e}I_3+Z_{0e}I_4+Z_{0o}I_3-Z_{0o}I_4)\csc\theta \end{align}$$

Symmetry can be used to derive other parameters.

Method 2

The mixed-mode S parameter of the coupled transmission line can be written as:

$$\mathbf{Z^{mm}}= \left[ \begin{matrix} -j2Z_{0o}\cot\theta & -j2Z_{0o}\csc\theta & {0} & {0} \\ -j2Z_{0o}\csc\theta & -j2Z_{0o}\cot\theta & {0} & {0} \\ {0} & {0} & \frac{-jZ_{0e}\cot\theta}{2} & \frac{-jZ_{0e}\csc\theta}{2} \\ {0} & {0} & \frac{-jZ_{0e}\cot\theta}{2} & \frac{-jZ_{0e}\csc\theta}{2} \end{matrix} \right]$$

Because the line is TEM, the propagation constant and phase velocity are the same for both of these modes $v_p=\omega/\beta=1/\sqrt{L_eC_e}=1/\sqrt{L_oC_o}$.

With the conversion formula listed in Appendix, we may write the standard S parameter as:

$$\mathbf{Z^{std}}=-j\left[ \begin{matrix} Z_p\cot\theta & Z_m\cot\theta & Z_m\csc\theta & Z_p\csc\theta \\ Z_m\cot\theta & Z_p\cot\theta & Z_p\csc\theta & Z_m\csc\theta \\ Z_m\csc\theta & Z_p\csc\theta & Z_p\cot\theta & Z_m\cot\theta \\ Z_p\csc\theta & Z_m\csc\theta & Z_m\cot\theta & Z_p\cot\theta \end{matrix} \right]$$

where $Z_p=(Z_{0e}+Z_{0o})/2,Z_m=(Z_{0e}-Z_{0o})/2$. Note that the port definition of port 3 and port 4 are opposite in Appendix and the aforementioned analysis. To make the conclusion compatible, the transformation is modified as

$$\mathbf{Z^{std}}=\mathbf{T}\mathbf{M}^{H}\mathbf{Z^{mm}}\mathbf{M}\mathbf{T}\\ \mathbf{T}=\left[ \begin{matrix} {1} & {0} & {0} & {0} \\ {0} & {1} & {0} & {0} \\ {0} & {0} & {0} & {1} \\ {0} & {0} & {1} & {0} \end{matrix} \right]$$

The additional matrix $\mathbf{T}$ is used to swap port sequence.

The Y parameter can be expressed as

$$\mathbf{Y}=-j\left[ \begin{matrix} {Y_p\cot\theta} & {-Y_m\cot\theta} & {Y_m\csc\theta} & {-Y_p\csc\theta} \\ {-Y_m\cot\theta} & {Y_p\cot\theta} & {-Y_p\csc\theta} & {Y_m\csc\theta} \\ {Y_m\csc\theta} & {-Y_p\csc\theta} & {Y_p\cot\theta} & {-Y_m\cot\theta} \\ {-Y_p\csc\theta} & {Y_m\csc\theta} & {-Y_m\cot\theta} & {Y_p\cot\theta} \end{matrix} \right]$$

where $Y_p=(Y_{0o}+Y_{0e})/2,Y_m=(Y_{0o}-Y_{0e})/2$.

Two-Port Configuration

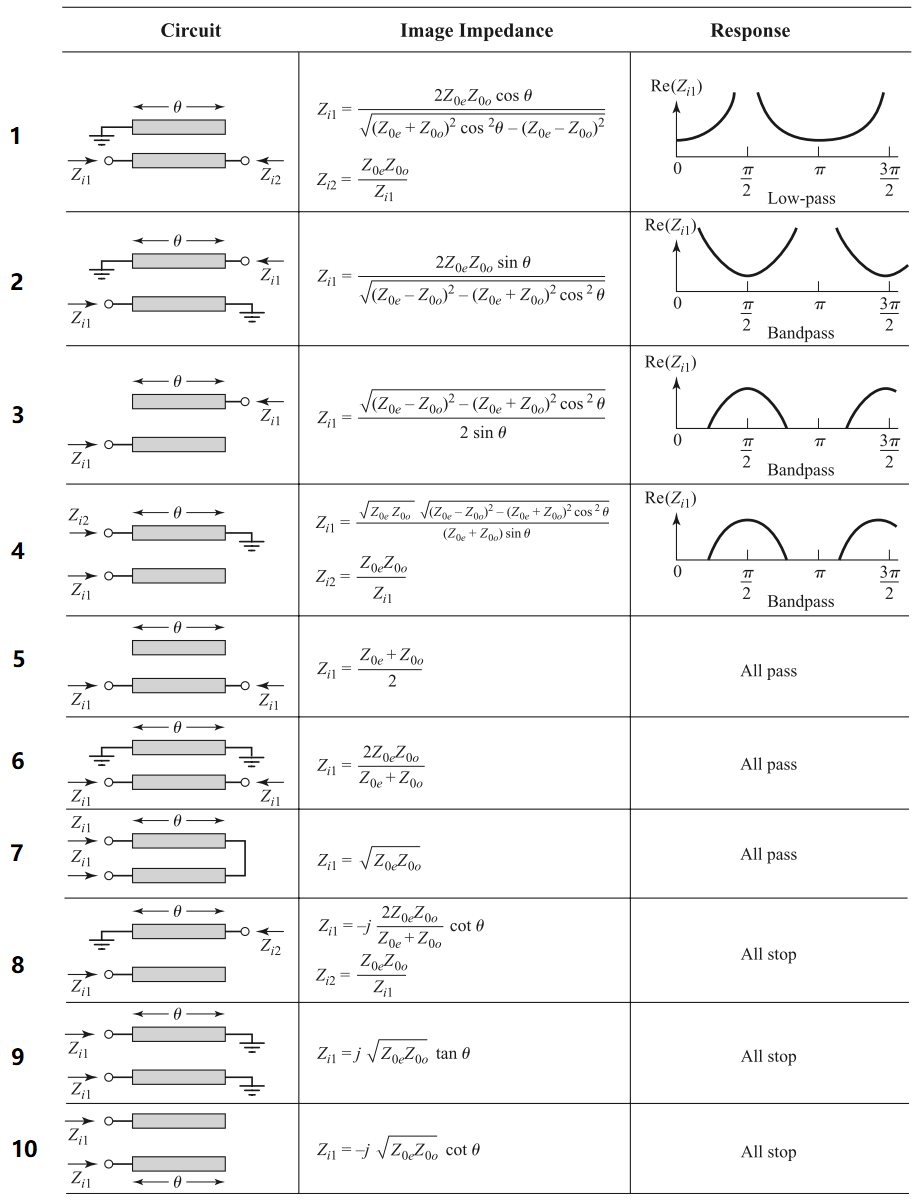
Type 3

Port 2 open

Port 4 open

$$\mathbf{Z}= \left[ \begin{matrix} -\frac{j}{2}(Z_{0e}+Z_{0o})\cot\theta & -\frac{j}{2}(Z_{0e}-Z_{0o})\csc\theta\\ -\frac{j}{2}(Z_{0e}-Z_{0o})\csc\theta & -\frac{j}{2}(Z_{0e}+Z_{0o})\cot\theta \\ \end{matrix} \right]$$

Type 5

Port 2 open

Port 3 open

$$\mathbf{Z}=\frac{Z_{0e}+Z_{0o}}{2} \left[ \begin{matrix} -j\cot\theta & -j\csc\theta\\ -j\csc\theta & -j\cot\theta \\ \end{matrix} \right]$$

Type 6

Port 2 short

Port 3 short

$$\mathbf{Z}=\frac{2Z_{0e}Z_{0o}}{Z_{0e}+Z_{0o}} \left[ \begin{matrix} -j\cot\theta & -j\csc\theta\\ -j\csc\theta & -j\cot\theta \\ \end{matrix} \right]$$

Type 7

Port 2-3 connected

$$\mathbf{Z}=-\frac{j}{2}\csc\theta \sec\theta\left[ \begin{matrix} Z_p\cos 2\theta +Z_m & Z_m\cos 2\theta +Z_p \\ Z_m\cos 2\theta +Z_p & Z_p\cos 2\theta +Z_m \\ \end{matrix} \right]$$

Type 8

Port 2 short

Port 4 open

$$\mathbf{Z}= \left[ \begin{matrix} -2j\frac{Z_{0e}Z_{0o}\cot\theta}{Z_{0e}+Z_{0o}} & 0\\ 0 & \frac{j}{2}(Z_{0e}+Z_{0o})\tan\theta \\ \end{matrix} \right]$$

It is an all-stop filter. An intuitive understanding is that when applied at the input, the signal is divided to the through and coupled ports, got reflected at these ports with open/short terminations, and out-of-phase combined at the isolation port, resulting in zero transmissions at all frequencies.

Appendix

Conversion Between the Standard S Parameter and Mixed-Mode S Parameter

Numbering of the ports is as follows:

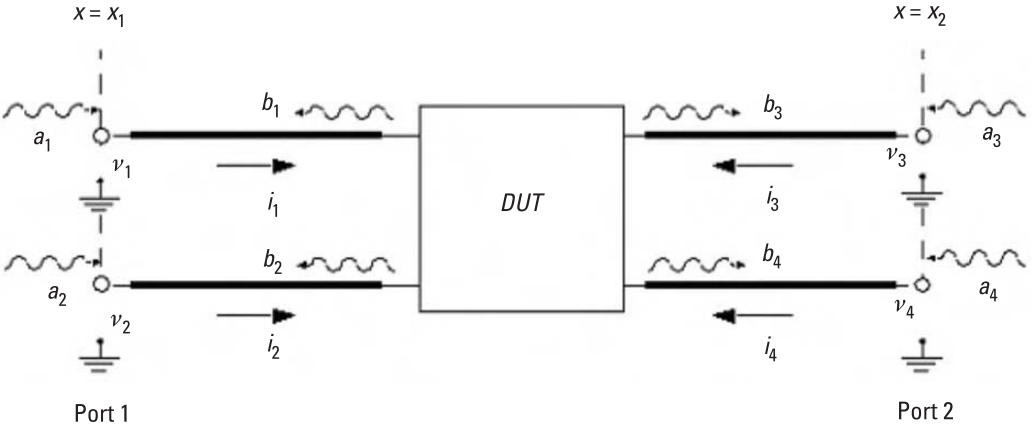
The standard S parameter ($\mathbf{S^{std}}$) is

$$\left[ \begin{matrix} {b_{1}} \\ {b_{2}} \\ {b_{3}} \\ {b_{4}} \end{matrix} \right] = \left[ \begin{matrix} {S_{11}} & {S_{12}} & {S_{13}} & {S_{14}} \\ {S_{21}} & {S_{22}} & {S_{23}} & {S_{24}} \\ {S_{31}} & {S_{32}} & {S_{33}} & {S_{34}} \\ {S_{41}} & {S_{42}} & {S_{43}} & {S_{44}} \end{matrix} \right] \left[ \begin{matrix} {a_{1}} \\ {a_{2}} \\ {a_{3}} \\ {a_{4}} \end{matrix} \right]$$

The mixed-mode S parameter ($\mathbf{S^{mm}}$) is:

$$\begin{aligned} \left[ \begin{matrix} {b_{d1}} \\ {b_{d2}} \\ {b_{c1}} \\ {b_{c2}} \end{matrix} \right] &= \left[ \begin{matrix} \mathbf{S_{dd}} & \mathbf{S_{dc}} \\ \mathbf{S_{cd}} & \mathbf{S_{cc}} \end{matrix} \right] \left[ \begin{matrix} {a_{d1}} \\ {a_{d2}} \\ {a_{c1}} \\ {a_{c2}} \end{matrix} \right]\\ &= \left[ \begin{matrix} {S_{dd11}} & {S_{dd12}} & {S_{dc11}} & {S_{dc12}} \\ {S_{dd21}} & {S_{dd22}} & {S_{dc21}} & {S_{dc22}} \\ {S_{cd11}} & {S_{cd12}} & {S_{cc11}} & {S_{cc12}} \\ {S_{cd21}} & {S_{cd22}} & {S_{cc21}} & {S_{cc22}} \end{matrix} \right] \left[ \begin{matrix} {a_{d1}} \\ {a_{d2}} \\ {a_{c1}} \\ {a_{c2}} \end{matrix} \right] \end{aligned}$$

The relationship between the two is:

$$\mathbf{S^{mm}}=\mathbf{M}\mathbf{S^{std}}\mathbf{M}^{H}\\ \mathbf{M}=\frac{1}{\sqrt{2}} \left[ \begin{matrix} {1} & {-1} & {0} & {0} \\ {0} & {0} & {1} & {-1} \\ {1} & {1} & {0} & {0} \\ {0} & {0} & {1} & {1} \end{matrix} \right]\\ \mathbf{M}\mathbf{M}^{H}=\mathbf{I}$$

Conversion Between the Standard Z Parameter and Mixed-Mode Z Parameter

For the full circuit, we may write

$$v_d=v_1-v_2\\ i_d=\frac{1}{2}(i_1-i_2)\\ v_c=\frac{1}{2}(v_1+v_2)\\ i_c=i_1+i_2$$

This is different from the half circuit analysis. The above equations can be put into matrix form.

$$\left[ \begin{matrix} {I_{d1}} \\ {I_{d2}} \\ {I_{c1}} \\ {I_{c2}} \end{matrix} \right] = \left[ \begin{matrix} {1/2} & {-1/2} & {0} & {0} \\ {0} & {0} & {1/2} & {-1/2}\\ {1} & {1} & {0} & {0} \\ {0} & {0} & {1} & {1} \end{matrix} \right] \left[ \begin{matrix} {I_{1}} \\ {I_{2}} \\ {I_{3}} \\ {I_{4}} \end{matrix} \right] \\ \left[ \begin{matrix} {U_{d1}} \\ {U_{d2}} \\ {U_{c1}} \\ {U_{c2}} \end{matrix} \right] = \left[ \begin{matrix} {1} & {-1} & {0} & {0} \\ {0} & {0} & {1} & {-1}\\ {1/2} & {1/2} & {0} & {0} \\ {0} & {0} & {1/2} & {1/2} \end{matrix} \right] \left[ \begin{matrix} {U_{1}} \\ {U_{2}} \\ {U_{3}} \\ {U_{4}} \end{matrix} \right]$$

which leads to

$$\mathbf{Z^{std}}=\mathbf{M}^{H}\mathbf{Z^{mm}}\mathbf{M}\\ \mathbf{M}=\left[ \begin{matrix} {1/2} & {-1/2} & {0} & {0} \\ {0} & {0} & {1/2} & {-1/2}\\ {1} & {1} & {0} & {0} \\ {0} & {0} & {1} & {1} \end{matrix} \right]$$

Instead if half circuit is used, we have

$$v_o=\frac{1}{2}(v_1-v_2)\\ i_o=\frac{1}{2}(i_1-i_2)\\ v_e=\frac{1}{2}(v_1+v_2)\\ i_e=\frac{1}{2}(i_1+i_2)$$

The result is modified to be the same as the S parameter.

Mathematica Derivation

Calculation of standard S parameter

Zmm = ( {
    {-2 I Zo Cot[t], -2 I Zo Csc[t], 0, 0},
    {-2 I Zo Csc[t], -2 I Zo Cot[t], 0, 0},
    {0, 0, -I/2 Ze Cot[t], -I/2 Ze Csc[t]},
    {0, 0, -I/2 Ze Csc[t], -I/2 Ze Cot[t]}
   } );
M = ({
    {1/2, -1/2, 0, 0},
    {0, 0, 1/2, -1/2},
    {1, 1, 0, 0},
    {0, 0, 1, 1}
   });
T = ( {
    {1, 0, 0, 0},
    {0, 1, 0, 0},
    {0, 0, 0, 1},
    {0, 0, 1, 0}
   } );
Zstd = T.Transpose[M].Zmm.M.T // MatrixForm

Derivation of type 6

St = ( {
   {a, d, b, c},
   {d, a, c, b},
   {b, c, a, d},
   {c, b, d, a}
  } ); y = ( {
   {V1},
   {V2},
   {V3},
   {V4}
  } ); x = ( {
   {I1},
   {I2},
   {I3},
   {I4}
  } );
result = Solve[(y /. {V2 -> 0, V3 -> 0}) == St.x, {V1, I2, I3, V4}][[1]];
Y = Simplify[( {
      {Coefficient[V1 /. result, I1], Coefficient[V1 /. result, I4]},
      {Coefficient[V4 /. result, I1], Coefficient[V4 /. result, I4]}
     } ) /. {a -> -(1/2) I Ze Cot[t] - 1/2 I Zo Cot[t], 
     b -> -(1/2) I Ze Csc[t] + 1/2 I Zo Csc[t], 
     c -> -(1/2) I Ze Csc[t] - 1/2 I Zo Csc[t], 
     d -> -(1/2) I Ze Cot[t] + 1/2 I Zo Cot[t]}];

Derivation of type 7

St = ( {
   {a, d, b, c},
   {d, a, c, b},
   {b, c, a, d},
   {c, b, d, a}
  } ); y = ( {
   {V1},
   {V2},
   {V3},
   {V4}
  } ); x = ( {
   {I1},
   {I2},
   {I3},
   {I4}
  } );
result = Solve[(y /. {V4 -> V3}) == (St.x /. I4 -> -I3), {V1, V2, I3, 
   V3}];
Y = Simplify[( {
      {Coefficient[(V1 /. result)[[1]], I1], 
       Coefficient[(V1 /. result)[[1]], I2]},
      {Coefficient[(V2 /. result)[[1]], I1], 
       Coefficient[(V2 /. result)[[1]], I2]}
     } ) /. {a -> -(1/2) I Ze Cot[t] - 1/2 I Zo Cot[t], 
     b -> -(1/2) I Ze Csc[t] + 1/2 I Zo Csc[t], 
     c -> -(1/2) I Ze Csc[t] - 1/2 I Zo Csc[t], 
     d -> -(1/2) I Ze Cot[t] + 1/2 I Zo Cot[t]}] ;
Y // MatrixForm

Parameter Extraction of the Coupled Transmission Line

Method 1

When configured in a way like this

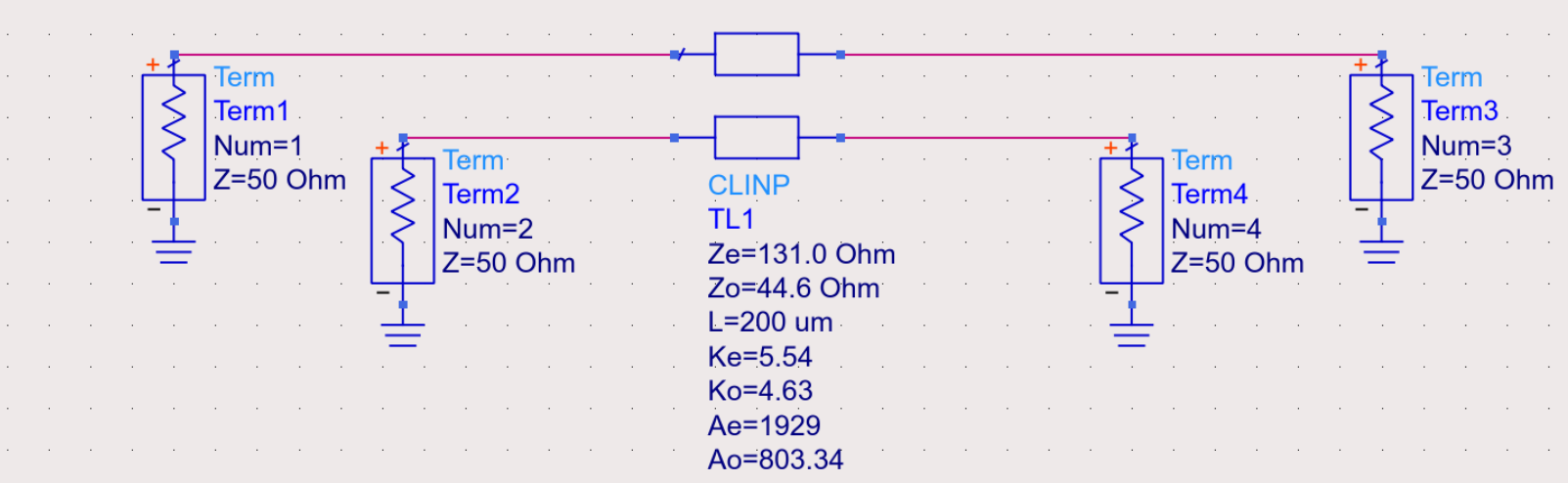
The S parameter of it should appear like

S = [a, b, c, d
    b, a, d, c
    c, d, a, b
    d, c, b, a];

It is then converted using Matlab, as

polar2complex = @(mag, pha) mag .* exp(1i*pha*pi/180);
a = polar2complex(0.141, 68.196);
b = polar2complex(0.171, 66.122);
c = polar2complex(0.951, -20.174);
d = polar2complex(0.083, -128.593);

S = [a, b, c, d
    b, a, d, c
    c, d, a, b
    d, c, b, a];

% convert to mixed-mode S parameter
M = 1/sqrt(2)*[1 -1 0 0
    0 0 1 -1
    1 1 0 0
    0 0 1 1];
Smm=M*S*M';

length = 200e-6;	% length of transmission line
freq = 30e9;		% frequency of simulation
Z0 = 50;			% characteristic impedance of the ports
C = 3e8;			% speed of light in free space

differential = s2rlgc(Smm(1:2,1:2), length, freq, Z0)
Zo = real(differential.Zc)
Ao = differential.alpha*8.686
Ko = (C*differential.beta/2/pi/freq)^2
common = s2rlgc(Smm(3:4,3:4), length, freq, Z0)
Ze = real(common.Zc)
Ae = common.alpha*8.686
Ke = (C*common.beta/2/pi/freq)^2

Method 2

Alternatively, the mixed-mode parameter can be obtained from direct simulation. For the even/common mode

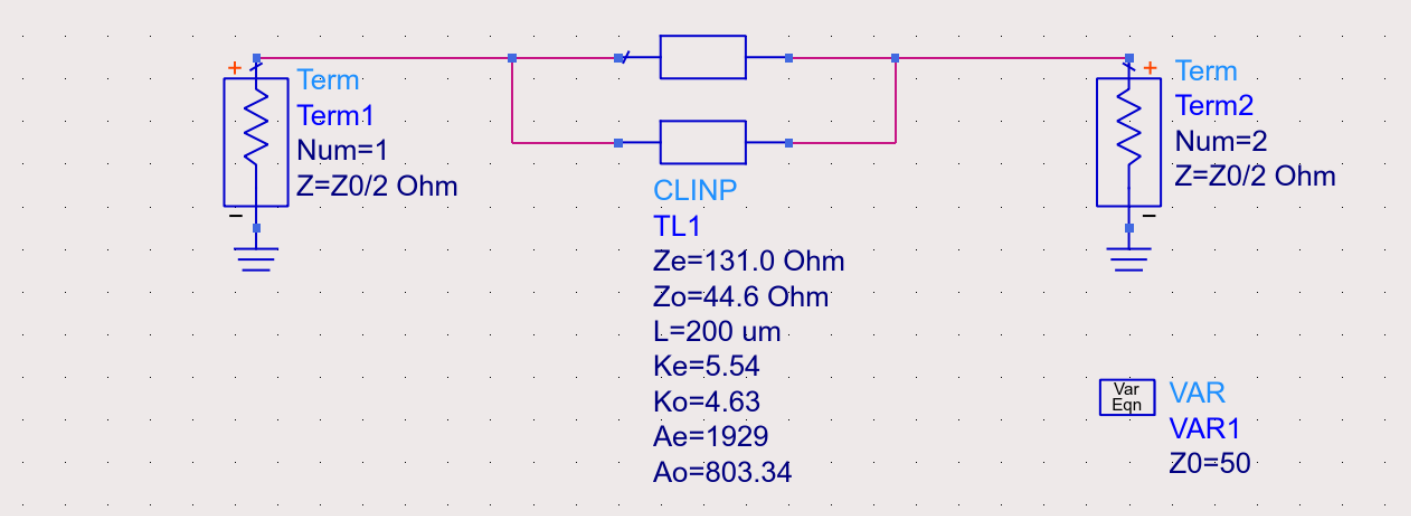
For the odd/differential mode

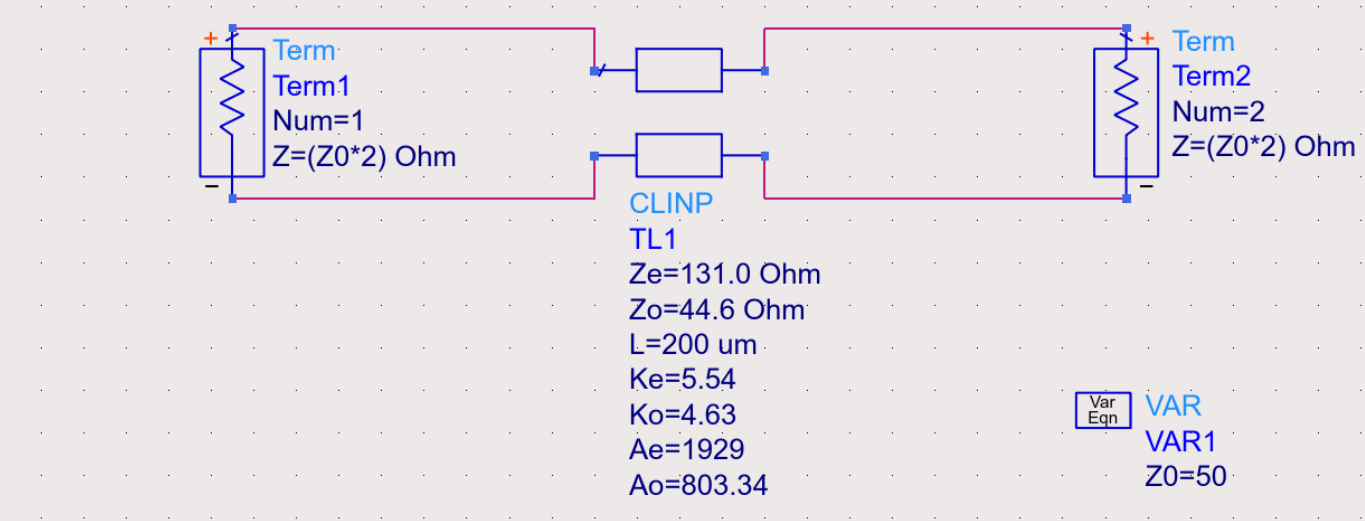
Note that the port impedance is changed accordingly.

Reference

For the derivation of coupled transmission line, Wilkinson power divider, quadrature hybrid, refer to

• D. M. Pozar, Microwave Engineering. NJ, Hoboken: Wiley, 1998.

For the conversion between the standard S parameter and mixed-mode S parameter, refer to

• W. R. Eisenstadt, B. Stengel and B. M. Thompson, Microwave Differential Circuit Design Using Mixed-Mode S-Parameters. Norwood: Artech House, 2006