Class F Power Amplifier

This article is about the design of class F power amplifier.

Assumption

Strong non-linearity assumption

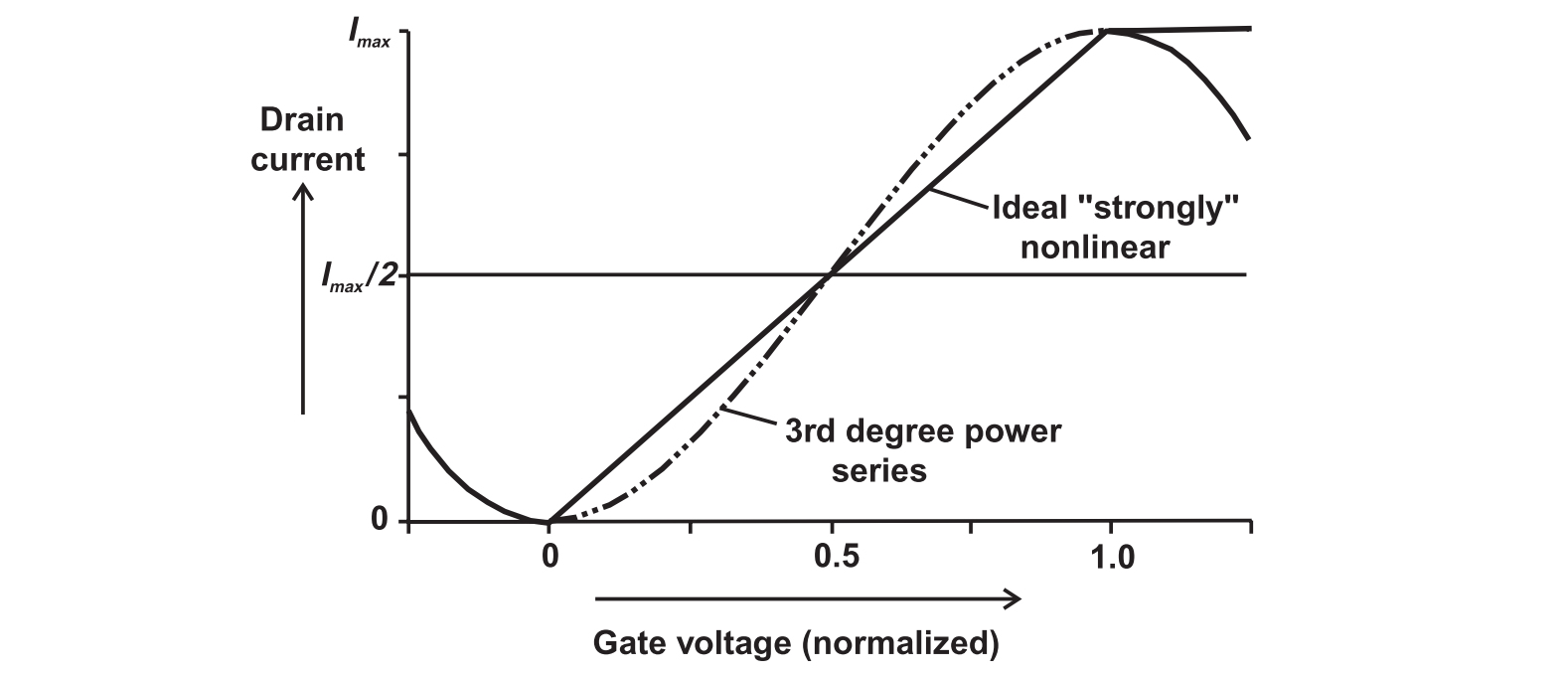
Overdriven Class A Amplifier

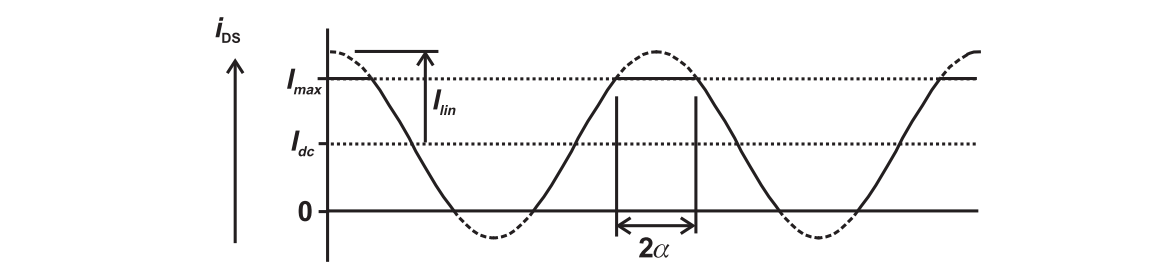
The clipping angle is defined as

$$I_{dc}+I_{lin}\cos\alpha=I_{max}\\ \cos\alpha=\frac{I_{max}}{2I_{lin}}$$

Thus, we may define the clipped cosine wave as

$$\begin{aligned} i(\theta) &= I_{max} &&0<\theta<\alpha,2\pi-\alpha<\theta<2\pi\\ &= \frac{1}{2}I_{max}+I_{lin}\cos\theta &&\alpha<\theta<\pi-\alpha,\pi+\alpha<\theta<2\pi-\alpha\\ &=0 && \pi-\alpha<\theta<\pi+\alpha \end{aligned}$$

Using Fourier series, we can obtain

$$I_1=I_{max} \cdot \frac{2}{\pi} \cdot \frac{\sin2\alpha+\pi-2\alpha}{4\cos\alpha}$$

r = 2/Pi Integrate[Imax Cos[x], {x, 0, a}] + 
 2/Pi Integrate[(0.5 Imax + Ilin Cos[x]) Cos[x], {x, a, Pi - a}]
I1 = Simplify[r /. Ilin -> Imax/2/Cos[a]]
(* (Imax Sec[a] (-2 a + \[Pi] + Sin[2 a]))/(2 \[Pi]) *)

The fundamental power and the maximal linear power are defined as

$$P_{rf}=\frac{I_1^2}{2R_L}\\ P_{lin}=\frac{I_{max}^2}{8R_L}$$

The power compression curve can be plotted as ($I_{max}$ and $R_L$ are normalized)

r = 2/Pi Integrate[Imax Cos[x], {x, 0, a}] + 
  2/Pi Integrate[(0.5 Imax + Ilin Cos[x]) Cos[x], {x, a, Pi - a}]
I1 = Simplify[r /. a -> ArcCos[Imax/2/Ilin]]
LogLogPlot[
 Piecewise[{{I1, Ilin > Imax/2}, {Ilin, Ilin < Imax/2}}] /. 
  Imax -> 1, {Ilin, 0.2, 2}, 
 AxesLabel -> {"Input Power", "Output Power"}, PlotRange -> All]

and the efficiency

LogLinearPlot[
 Piecewise[{{(I1^2/2)/(Imax^2/4), 
     Ilin > Imax/2}, {(Ilin^2/2)/(Imax^2/4), Ilin < Imax/2}}] /. 
  Imax -> 1, {Ilin, 0.2, 2}, 
 AxesLabel -> {"Input Power", "Efficiency"}, PlotRange -> All]

It can be observed at 1-dB compression point, more power is extracted with no extra DC consumption, achieving an efficiency of 63 %. The maximal efficiency is $8/\pi^2$, where a infinite $I_{lin}$ is required. Hence, we can trade linearity for efficiency.

Overdriven Class AB Amplifier

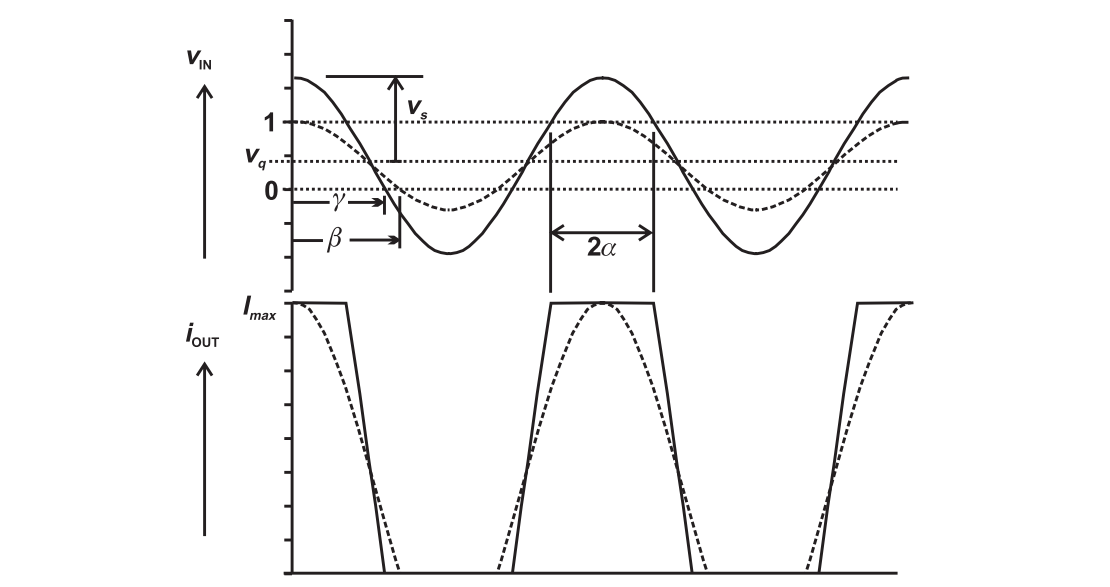
In the analysis, the transconductance is assumed to be 1. The nominal conduction angle is

$$\cos\beta=\frac{v_q}{v_q-1}\\$$

The maximal linear amplitude is

$$v_{lin}=1-v_q$$

The overdriven conduction angle is

$$\cos\gamma=-\frac{v_q}{v_s}$$

The clipping angle is given by

$$\cos\alpha=\frac{1-v_q}{v_s}$$

The device output current is

$$\begin{aligned} i(\theta) &= 1 &&0<\theta<\alpha,2\pi-\alpha<\theta<2\pi\\ &= v_q+v_s\cos\theta &&\alpha<\theta<\gamma,2\pi-\gamma<\theta<2\pi-\alpha\\ &=0 && \gamma<\theta<2\pi-\gamma \end{aligned}$$

Adopting Fourier series, we have

$$I_{dc}=\frac{1}{\pi}\int_{0}^{\pi}i(\theta)\ d\theta\\ I_{1}=\frac{2}{\pi}\int_{0}^{\pi}i(\theta)\cos\theta\ d\theta$$

Different from the above analysis, the voltage waveform is assumed to be cosine wave with peak amplitude $V_{dc}$.

$$P_{rf}=\frac{V_{dc}I_1}{2}\\ P_{dc}=V_{dc}I_{dc}\\ \eta=\frac{I_1}{2I_{dc}}$$

Efficiency

Power

vq = Cos[b]/(Cos[b] - 1);
g = ArcCos[-vq/vs];
a = ArcCos[(1 - vq)/vs];
Idc = 1/Pi Integrate[1, {x, 0, a}] + 
   1/Pi Integrate[vq + vs Cos[x], {x, a, g}];
I1 = 2/Pi Integrate[Cos[x], {x, 0, a}] + 
   2/Pi Integrate[(vq + vs Cos[x]) Cos[x], {x, a, g}];
eta = I1/2/Idc;

(* plot efficiency *)
Plot[{eta /. vs -> (1 - vq), eta /. vs -> (1 - vq) 10^0.1, 
  eta /. vs -> (1 - vq) 10^0.2, eta /. vs -> (1 - vq) 10^0.3}, {b, 
  0.01, Pi}, AxesLabel -> {"Conduction Angle", "Efficiency"}, 
 PlotLegends -> {"0 dB", "2 dB", "4 dB", "6 dB"}]
 
(* plot power *)
I1dB = 20 Log10[I1*2];
Plot[{I1dB /. vs -> (1 - vq), I1dB /. vs -> (1 - vq) 10^0.1, 
  I1dB /. vs -> (1 - vq) 10^0.2, I1dB /. vs -> (1 - vq) 10^0.3}, {b, 
  0.01, Pi}, AxesLabel -> {"Conduction Angle", "Power"}, 
 PlotLegends -> {"0 dB", "2 dB", "4 dB", "6 dB"}]

For class AB and class A amplifier, input overdrive can increase the efficiency and the output power simultaneously; for class B amplifier the power improvement is offset by a reduction in efficiency; for class C amplifier, the increase in power is dramatic while the efficiency decreases slightly.

Class F Amplifier

Addition of third order in-phase harmonic can lower the peak amplitude.

Assume a waveform of

$$v(\theta)=\cos\theta-k\cos3\theta$$

For

1. $k<1/9$, there will be a single peak
2. $k=1/6$, the peak amplitude reaches global minimum
3. $k>1/2.5$, the peak amplitude raises beyond 1

Assuming a class B operation, the efficiency improvement is calculated as

D[Cos[x] - k Cos[3 x], x]
Solve[-Sin[x] + 3 k Sin[3 x] == 0 && 0 < x < \[Pi]/2 && 1 > k > 1/9,
  x]
Vpk = Piecewise[{{1 - k, 
     k <= 1/9}, {Cos[x] - k Cos[3 x] /. 
      x -> 1/2 ArcCos[(1 - 3 k)/(6 k)], k > 1/9}}];
Plot[{Vpk, 10 Log10[1/Vpk], Pi/4/Vpk}, {k, 0, 0.5}, 
 PlotLegends -> {"Peak Value", "Power Increase [dB]", "Efficiency"}]

Consider the maximal flat condition where $k=1/9$, the power improvement is 1.125, and the efficiency is 88.4 %. It is illustrated by the following figure.

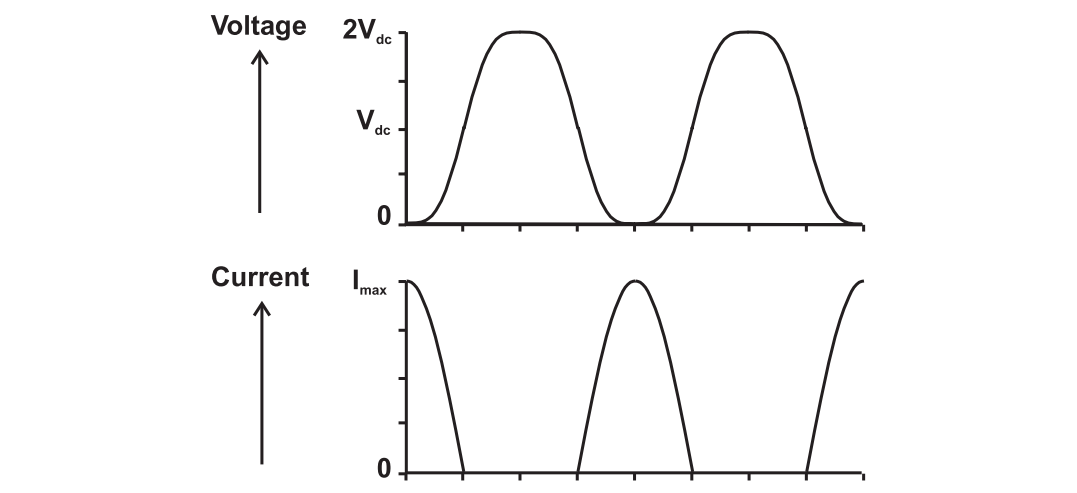
In the configuration, the current waveform is half-wave rectified sinewave, and the voltage is maximally flat third harmonically enhanced sinewave. It can be called class F operation.

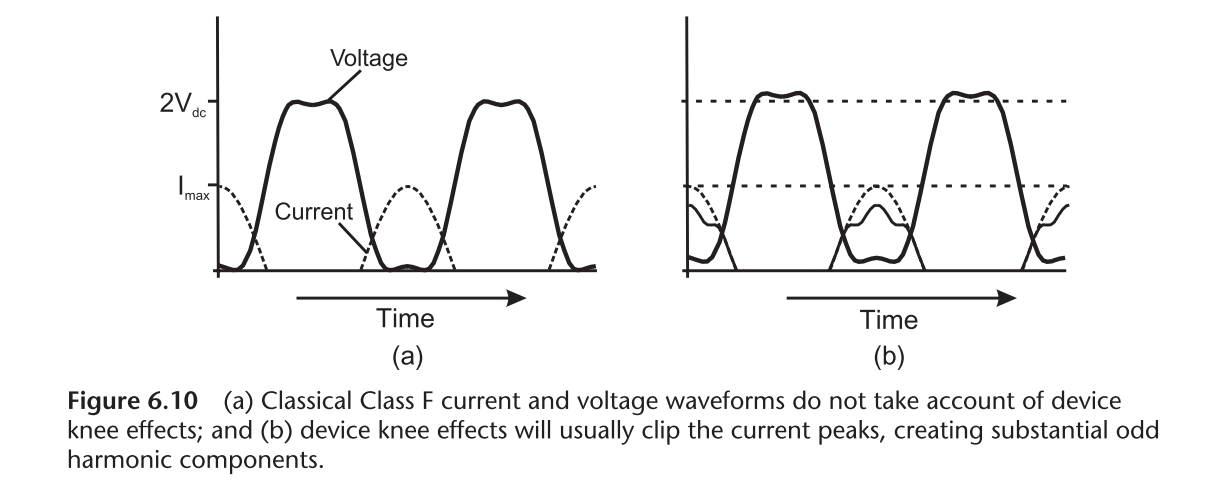
However, a half-wave rectified sine wave has no odd harmonics. To generate a voltage waveform with third order harmonic, the circuit must see an infinite third harmonic impedance, which is unrealizable. In reality, the action of the device knee region is to clip the peaks of the current wave, thus generating substantial amounts of third harmonic.

Class FD Amplifier

Instead of manipulating odd harmonic impedance, the desired waveform can be obtain through clipping.

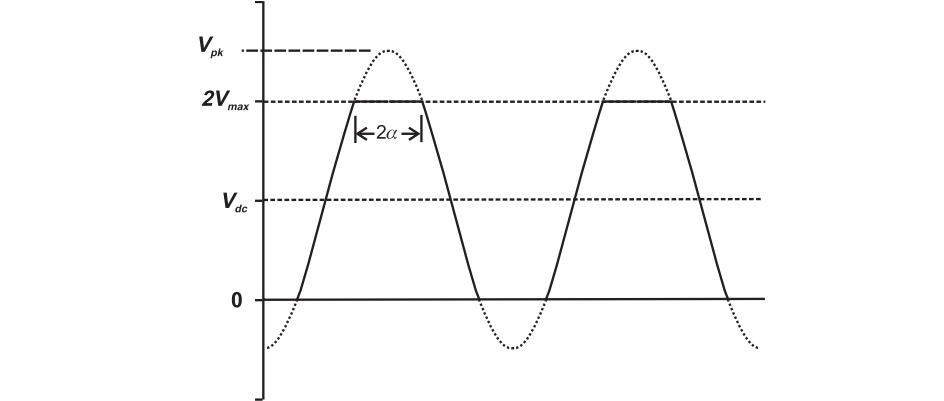
The schematic is as follows

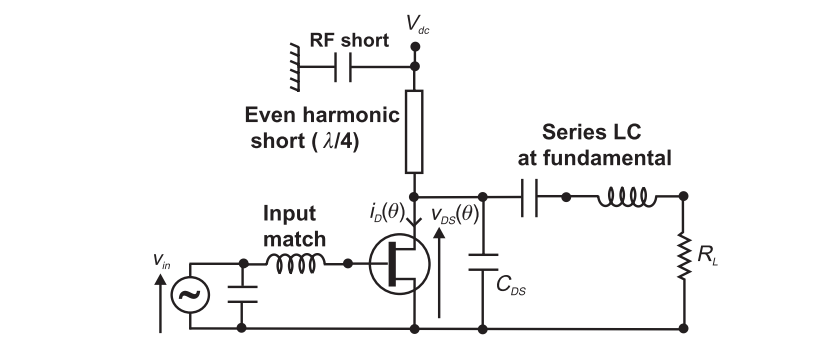
The key elements are

1. SCSS even harmonic short
2. Fundamental load, whose value is deliberately higher
3. Series LC resonator at the fundamental to present open circuit at higher odd harmonics

The voltage waveform should be a sinewave with amplitude of $I_{max}R_L/2$. It would attempt to clip at zero and $2V_{dc}$. The even harmonic short-circuit forces the upper clipping to mirror the actual physical clipping which occurs in the knee region.

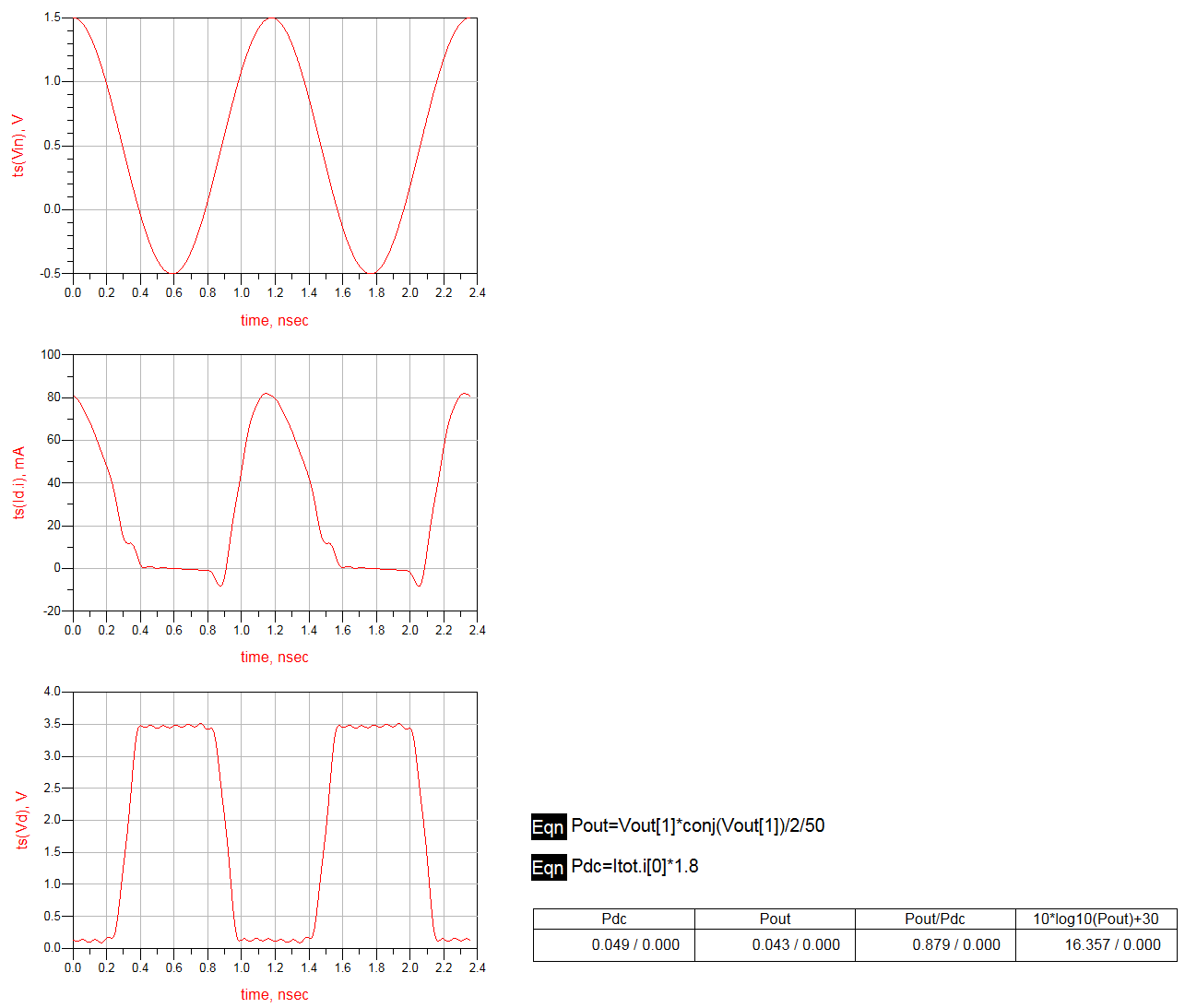
Reference

1. S. C. Cripps. RF Power Amplifier for Wireless Communications. Artech House, 2014.