Class J Power Amplifier

This article includes a brief introduction to the class J PA.

Harmonic Short Termination

Equal Harmonic Termination

In the analysis from class A to class C PA, it is assumed the load can provide a short at higher harmonics. If this assumption cannot hold, the efficiency of the power amplifier will reduce. The waveform in the following figure is a class B PA with harmonic short. Ideally, it can achieve a drain efficiency of $\pi/4$ , or approximately 78.5%.

In the figure, current is normalized to $I_{max}$, while voltage is normalized to $2V_{dd}$.

For a class B PA with the same impedance across all harmonics, it should assume a waveform as follows. When the load impedance is modified so as to make voltage average equal to $V_{dd}$, it has an efficiency of $\pi^2/(8-8\pi)$, or approximately 57.6%.

Therefore, without harmonic short, the efficiency of traditional PA is greatly reduced.

The output capacitance of the device $C_{ds}$ reduces the load impedance at high frequency, and thus can be considered as a approximation to ideal harmonic termination. Following this method, the reactance of the capacitor should be as low as possible. The metric $X_{C_{ds}}/R_L$ at the fundamental is defined to assess the approximation. If $X_{C_{ds}}/R_L\ll1$, the classic result can be expected. However, even if $X_{C_{ds}}/R_L>1$, with a substantial reactive component, the efficiency can be restored or even enhanced. This technique is called class J PA.

Capacitive Harmonic Termination

Due to the influence of $C_{ds}$, the voltage waveform is

$$v(\theta)=\cos\theta+v_2\sin 2\theta$$

Addition of the second harmonic would increase peak-to-peak range. If the peak voltage is kept the same, the fundamental component is reduced, thereby reducing the efficiency.

As shown in the figure below, a high $X_{C_{ds}}$ would lower the fundamental voltage, thereby reducing the efficiency achievable. On the other hand, however, a low $X_{C_{ds}}$ would increase the quality factor of the output node, and thus reducing the output bandwidth.

result = {};
For[Iq = 0, Iq <= 0.5, Iq += 0.1, Imax = 1;
 Ipk = Imax - Iq;
 alpha = 2 ArcCos[-Iq/Ipk];
 Id[t_] := 
  Piecewise[{{Imax (Cos[t] - Cos[alpha/2])/(1 - Cos[alpha/2]), -alpha/
       2 < t < alpha/2}, {0, True}}];
 Idc = 1/2/Pi Integrate[Id[t] , {t, -alpha/2, alpha/2}];
 I1 = 1/Pi Integrate[Id[t] Cos[t], {t, -alpha/2, alpha/2}];
 I2 = 1/Pi Integrate[Id[t] Cos[2 t], {t, -alpha/2, alpha/2}];
 eta = I1/2/Idc;
 x = Table[k, {k, 0, 5, 0.25}];
 y = Table[
   eta/Maximize[{Cos[t] + I2/I1 k/2 Sin[2 t], 0 < t < 2 Pi}, t][[
     1]], {k, x}];
 result = Append[result, Table[{x[[k]], y[[k]]}, {k, Length[x]}]]]
ListLinePlot[result, PlotRange -> {0.4, 0.8}, 
 PlotLegends -> {"Vq=0", "Vq=0.1", "Vq=0.2", "Vq=0.3", "Vq=0.4", 
   "Vq=0.5"}, AxesLabel -> {"Xcds/Rl", "Efficiency [%]"}]

Class J Power Amplifier

The class J power amplifier differs from classic amplifiers in that:

• The load is not purely resistive at the fundamental frequency
• The load presents high impedances at higher harmonics
• The output capacitance is used to provide a specific reactive termination at the second harmonic, generating a non-sinusoidal waveform.

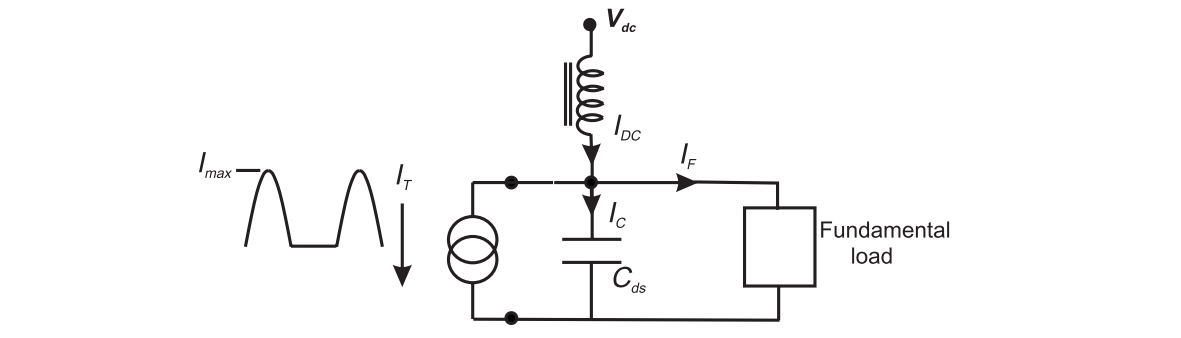
In the analysis, the transistor is assumed to be a current generator. In class B condition, it has a current of

$$\begin{aligned} I_T&=I_{max}\sin\theta &&0<\theta<\pi\\ &=0 &&\pi<\theta<2\pi \end{aligned}$$

The fundamental current flowing in the matching branch has the form

$$I_F=I_1\sin(\theta+\phi)$$

And thus the current flowing through the capacitor is

$$I_C=I_{DC}-I_T-I_F$$

Thus, the voltage can be obtained through integration

$$\begin{aligned} V_o(\theta) =&\frac{1}{\omega C}\int_0^\theta \left( \frac{I_{max}}{\pi}-I_{max}\sin\varphi-I_1\sin(\varphi+\phi) \right)d\varphi+V_{off} &&0<\theta<2\pi\\ =&\frac{1}{\omega C}\int_0^\pi \left( \frac{I_{max}}{\pi}-I_{max}\sin\varphi-I_1\sin(\varphi+\phi) \right)d\varphi\\ &+\frac{1}{\omega C}\int_\pi^\theta \left( \frac{I_{max}}{\pi}-I_1\sin(\varphi+\phi) \right)d\varphi+V_{off} &&\pi<\theta<2\pi \end{aligned}$$

where $V_{off}$ is an arbitrary offset to make $V_o(\theta)\ge0$, and $1/\omega C$ is adjusted to make the average of $V_o(\theta)$ equal to $V_{dd}$.

For instance, for $I_1=0.6,\phi=10.2^\circ$, calculated results are

Xcds (1/wC) = 7.69585
Xcds/Rl = 3.84793
Zl (with Cds) = 1.63538 +1.39322 I
Zl (without Cds) = 1.13568 +1.384 I
Zl/Rl (with Cds) = 0.817691 +0.696608 I
Zl/Rl (without Cds) = 0.567841 +0.692 I
efficiency = 0.642213
Prf = -0.874108

In the figure, current is normalized to $I_{max}$, while voltage is normalized to $V_{dd}$.

(*define the current and the voltage waveform*)
condition = {Imax -> 1, I1 -> 2, Phi -> (180 - 68.01)/180 Pi, 
   Xcds -> 1};
Io[t_] := Piecewise[{{Imax Sin[t], 0 < t < Pi}, {0, true}}];
Vo[t_] := 
  Piecewise[{{Xcds Integrate[
       Imax/Pi - Imax Sin[p] - I1 Sin[p + Phi], {p, 0, t}], 
     t <= Pi}, {Xcds Integrate[
        Imax/Pi - Imax Sin[p] - I1 Sin[p + Phi], {p, 0, Pi}] + 
      Xcds Integrate[Imax/Pi - I1 Sin[p + Phi], {p, Pi, t}], t > Pi}}];
(*set the parameters*)
a = Vo[t] /. condition;
b = Io[t] /. condition;
(*add suitable Voff to make Vo>0*)
min = Minimize[{a, 0 < t < 2 Pi}, t];
a = a - min[[1]];
(*scale the expression to make the mean value equal to 1*)
ave = Integrate[a, {t, 0, 2 Pi}]/2/Pi;
a = a/ave;
(*calculate Xcds/Rl,note that Rl equal to 2Vdd/Imax,or simply 2 after normalization*)
Print["Xcds (1/wC) = ", 1/ave]
Print["Xcds/Rl = ", 1/ave/2]
(*perform the fourier tranformation to obtain the in-phase and quadrature component*)
(*note that the current is reversed to represent the one flow through the load*)
SinCoe = 1/Pi Integrate[a Sin[t], {t, 0, 2 Pi}];
CosCoe = 1/Pi Integrate[a Cos[t], {t, 0, 2 Pi}];
Print["Zl (with Cds) = ", (CosCoe - I SinCoe)/(1/2 I)]
Print["Zl (without Cds) = ", (CosCoe - I SinCoe)/
    I1/(Sin[Phi] - I Cos[Phi]) /. condition ]
Print["Zl/Rl (with Cds) = ", (CosCoe - I SinCoe)/(1/2 I)/2]
Print["Zl/Rl (without Cds) = ", (CosCoe - I SinCoe)/
     I1/(Sin[Phi] - I Cos[Phi])/2 /. condition ]
(*calculate the efficiency and power*)
Print["efficiency = ", Abs[SinCoe] Pi/4]
Print["Prf = ", 10 Log10[Abs[SinCoe]]]
(*plot the waveforms*)
Plot[{a, b}, {t, 0, 2 Pi}, PlotLegends -> {"Vo", "Io"}]

Similarly, the analysis can be performed for several other occasions.

No.	I1	Phi	Xcds/Rl	Prf	Eff	R1	X1
1	2.0	112	0.27	0	78.5	1.0	0.13
2	0.7	164.4	2.65	0	78.5	1.0	0.92
3	0.6	10.2	3.82	-0.9	63.9	0.82	0.69

The key class J design maneuver is to shift the phasing of the voltage and current waveforms, without changing their shape, such that the second harmonic voltage and current components are in phase quadrature.