Useful Mathematical Formulas

This article will present:

• Identities
• Derivative formulas
• Integral formulas
• Taylor series
• Fourier transformation (include DTFT and DFT)
• Laplace transformation
• Z transformation

Identities

$$\begin{aligned} \csc x &= \frac{1}{\sin x}\\ \sec x &= \frac{1}{\cos x}\\ \cot x &= \frac{1}{\tan x}\\ e^{jx} &= \cos x+j\sin x\\ \cos x &= \frac{e^{jx}+e^{-jx}}{2}=\cosh jx\\ \sin x &= \frac{e^{jx}-e^{-jx}}{2j}=\frac{1}{j}\sinh jx\\ \tan x &= \frac{1}{j}\frac{e^{jx}-e^{-jx}}{e^{jx}+e^{-jx}}=\frac{1}{j}\tanh jx\\ e^{x} &= \cosh x+\sinh x\\ \cosh x &= \frac{e^{x}+e^{-x}}{2}=\cos\frac{x}{j}\\ \sinh x &= \frac{e^{x}-e^{-x}}{2}=j\sin\frac{x}{j}\\ \tanh x &= \frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}=j\tan\frac{x}{j} \end{aligned}$$

Trigonometric Function

$$\begin{aligned} 1 &= \sin^2\alpha+\cos^2\alpha\\ &= \sec^2\alpha-\tan^2\alpha\\ &= \csc^2\alpha-\cot^2\alpha\\ \sin 2\alpha &= 2\sin \alpha \cos \alpha\\ \cos 2\alpha &= \cos^2 \alpha - \sin^2 \alpha\\ &= 2\cos^2 \alpha - 1\\ &= 1 - 2\sin^2 \alpha\\ \tan 2\alpha &= \frac{2\tan \alpha}{1-\tan^2\alpha}\\ \sin(\alpha\pm\beta) &=\sin\alpha\cos\beta\pm\cos\alpha\sin\beta\\ \cos(\alpha\pm\beta) &=\cos\alpha\cos\beta\mp\sin\alpha\sin\beta\\ \tan(\alpha\pm\beta) &=\frac{\tan\alpha\pm\tan\beta}{1\mp\tan\alpha\tan\beta}\\ \\ 1 &= \cosh^2\alpha-\sinh^2\alpha\\ \sinh 2\alpha &= 2\sinh \alpha \cosh \alpha\\ \cosh 2\alpha &= \cosh^2 \alpha + \sinh^2 \alpha\\ &= 2\cosh^2 \alpha - 1\\ &= 1 + 2\sinh^2 \alpha\\ \sinh(\alpha\pm\beta) &=\sinh\alpha\cosh\beta\pm\cosh\alpha\sinh\beta\\ \cosh(\alpha\pm\beta) &=\cosh\alpha\cosh\beta\pm\sinh\alpha\sinh\beta\\ \tanh(\alpha\pm\beta) &=\frac{\tanh\alpha\pm\tanh\beta}{1\pm\tanh\alpha\tanh\beta}\\ \end{aligned}$$

Sum-product conversion

$$\begin{aligned} \sin\alpha\sin\beta&=\frac{\cos(\alpha-\beta)-\cos(\alpha+\beta)}{2}\\ \cos\alpha\cos\beta&=\frac{\cos(\alpha-\beta)+\cos(\alpha+\beta)}{2}\\ \sin\alpha\cos\beta&=\frac{\sin(\alpha+\beta)+\sin(\alpha-\beta)}{2}\\ \cos\alpha\sin\beta&=\frac{\sin(\alpha+\beta)-\sin(\alpha-\beta)}{2}\\ \sin\alpha+\sin\beta&=2\sin\frac{\alpha+\beta}{2}\cos\frac{\alpha-\beta}{2}\\ \sin\alpha-\sin\beta&=2\cos\frac{\alpha+\beta}{2}\sin\frac{\alpha-\beta}{2}\\ \cos\alpha+\cos\beta&=2\cos\frac{\alpha+\beta}{2}\cos\frac{\alpha-\beta}{2}\\ \cos\alpha-\cos\beta&=-2\sin\frac{\alpha+\beta}{2}\sin\frac{\alpha-\beta}{2}\\ \tan\alpha+\tan\beta&=\frac{\sin\alpha+\sin\beta}{\cos\alpha\cos\beta}\\ \end{aligned}$$

Limits

$$\begin{aligned} \lim_{n\to\infty}\left(1+\frac{1}{n}\right)^n &= e \end{aligned}$$

Derivative Formulas

Theory

$$\begin{aligned} (uv)' &= u'v+uv'\\ \left(\frac{u}{v}\right)' &= \frac{u'v-uv'}{v^2}\\ \frac{dy}{dx} &= \frac{dy}{du}\cdot\frac{du}{dx}\\ \end{aligned}$$

Basic

$$\begin{aligned} (x^n)' &= nx^{n-1}\\ (\ln x)' &= \frac{1}{x}\\ (e^x)' &= e^x\\ (a^x)' &= a^x\ln a\\ \end{aligned}$$

Trigonometric Function

$$\begin{aligned} (\sin x)' &= \cos x\\ (\cos x)' &= -\sin x\\ (\tan x)' &= \sec^2x\\ (\sec x)' &= \sec x \tan x\\ (\csc x)' &= -\csc x \cot x\\ (\cot x)' &= -\csc^2x\\ (\arcsin x)' &= \frac{1}{\sqrt{1-x^2}}\\ (\arccos x)' &= -\frac{1}{\sqrt{1-x^2}}\\ (\arctan x)' &= \frac{1}{1+x^2}\\ \\ (\sinh x)' &= \cosh x\\ (\cosh x)' &= \sinh x\\ (\tanh x)' &= 1-\tanh^2x\\ \end{aligned}$$

Integral Formulas

Theory

Integration by substitution

$$\begin{aligned} \int f(x)dx &= \int g(\varphi(x))\varphi'(x)dx\\ &= \int g(u)du &\varphi(x)\to u\\ &=G(u)+C\\ &=G(\varphi(x))+C \end{aligned}$$

or

$$\begin{aligned} \int g(u)du &= \int g(\varphi(x))\varphi'(x)dx & u\to\varphi(x)\\ &= f(x)dx & g(\varphi(x))\varphi'(x)\to f(x)\\ &=F(x)+C\\ &=F(\varphi^{-1}(u))+C \end{aligned}$$

For finite integral

$$\int_a^bg(u)du=\int_\alpha^\beta g(\varphi(x))\varphi'(x)dx$$

when $a=\varphi(\alpha), b=\varphi(\beta)$

Integration by parts

$$\int u\ dv=uv-\int v\ du$$

Advanced

$$\begin{aligned} \int_0^\infty e^{-x^2}dx=\frac{\sqrt{\pi}}{2} \end{aligned}$$

Series

Arithmetic series

$$\begin{aligned} a_n &= a_1+(n-1)d\\ \sum_{k=1}^n a_k &= \frac{n(a_1+a_n)}{2}\\ &= \frac{n[2a_1+(n-1)d]}{2} \end{aligned}$$

Geometric series

$$\begin{aligned} b_n &= b_1 r^{n-1}\\ \sum_{k=1}^n b_k &= \frac{b_1-b_{n+1}}{1-r}\\ &= \frac{b_1(1-r^n)}{1-r}\\ \end{aligned}$$

Others

$$\begin{aligned} \sum_{k=1}^n \frac{1}{k(k+1)} &= \frac{n}{n+1}\\ \sum_{k=1}^n k(k+1) &= \frac{n(n+1)(n+2)}{3}\\ \sum_{k=1}^n k^2 &= \frac{n(n+1)(2n+1)}{6}\\ \end{aligned}$$

Taylor Expansion

Theory

$$\begin{aligned} f(x) &= f(x_0)+\sum_{k=1}^\infty\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n+R_n(x)\\ \end{aligned}$$

Example

$$\begin{aligned} e^x &= \sum_{k=0}^\infty \frac{x^k}{k!}\\ &= 1+\frac{1}{1!}x+\frac{1}{2!}x^2+o(x^2)\\ \frac{1}{1-x} &= \sum_{k=0}^\infty x^k\\ &= 1+x+x^2+o(x^2)\\(1+x)^a &= \sum_{k=0}^\infty \frac{a!}{k!(a-k)!}x^k\\ &= 1+\frac{a}{1!}x+\frac{a(a-1)}{2!}x^2+o(x^2)\\ \ln(1+x) &= \sum_{k=1}^\infty (-1)^{k+1}\frac{x^k}{k}\\ &= x-\frac{1}{2}x^2+\frac{1}{3}x^3+o(x^3)\\ \sin(x) &= \sum_{k=1}^\infty (-1)^{k+1}\frac{x^{2k-1}}{(2k-1)!}\\ &= x-\frac{1}{3!}x^3+\frac{1}{5!}x^5+o(x^5)\\ \cos(x) &= 1+\sum_{k=1}^\infty (-1)^{k}\frac{x^{2k}}{(2k)!}\\ &= 1-\frac{1}{2!}x^2+\frac{1}{4!}x^4+o(x^4)\\ e^{jx} &= \cos x+j\sin x\\ \end{aligned}$$

Fourier Series

Theory

Convolution

$$x(t)*y(t)=\int_{-\infty}^{\infty}y(\tau)x(t-\tau)d\tau$$

Complex exponentials as eigenfunctions (A signal for which the output of the system is a constant times the input)

$$\begin{aligned} y(t)&=\int_{-\infty}^{\infty}h(\tau)x(t-\tau)d\tau\\ &=\int_{-\infty}^{\infty}h(\tau)e^{s(t-\tau)}d\tau &x(t)=e^{st}\\ &=e^{st}\int_{-\infty}^{\infty}h(\tau)e^{-s\tau}d\tau \end{aligned}$$

Thus, we may express

$$x(t)=\sum_k a_ke^{s_kt}$$

If the signal is periodic for T

$$x(t+T)=x(t)\quad \text{for all }t.$$

Complex

when $T=2\pi/\omega_0$

$$x(t)=\sum_{k=-\infty}^{+\infty}a_ke^{jk\omega_0t}$$

where

$$a_k=\frac{1}{T}\int_Tx(t)e^{-jk\omega_0t}dt$$

Traditional

when $T=2\pi/\omega_0$

$$x(t)=\frac{a_0}{2}+\sum_{k=1}^\infty a_k\cos(k\omega_0t)+\sum_{k=1}^\infty b_k\sin(k\omega_0t)$$

where

$$a_k=\frac{2}{T}\int_Tx(t)\cos(k\omega_0t)dt\quad{k=0,1,...}\\ b_k=\frac{2}{T}\int_Tx(t)\sin(k\omega_0t)dt\quad{k=1,2,...}$$

Example

Periodic square wave

$$x(t)= \begin{cases} 1& kT-\tau/2<t<kT+\tau/2, k=0, \pm1, ...\\ 0& \text{else} \end{cases}$$

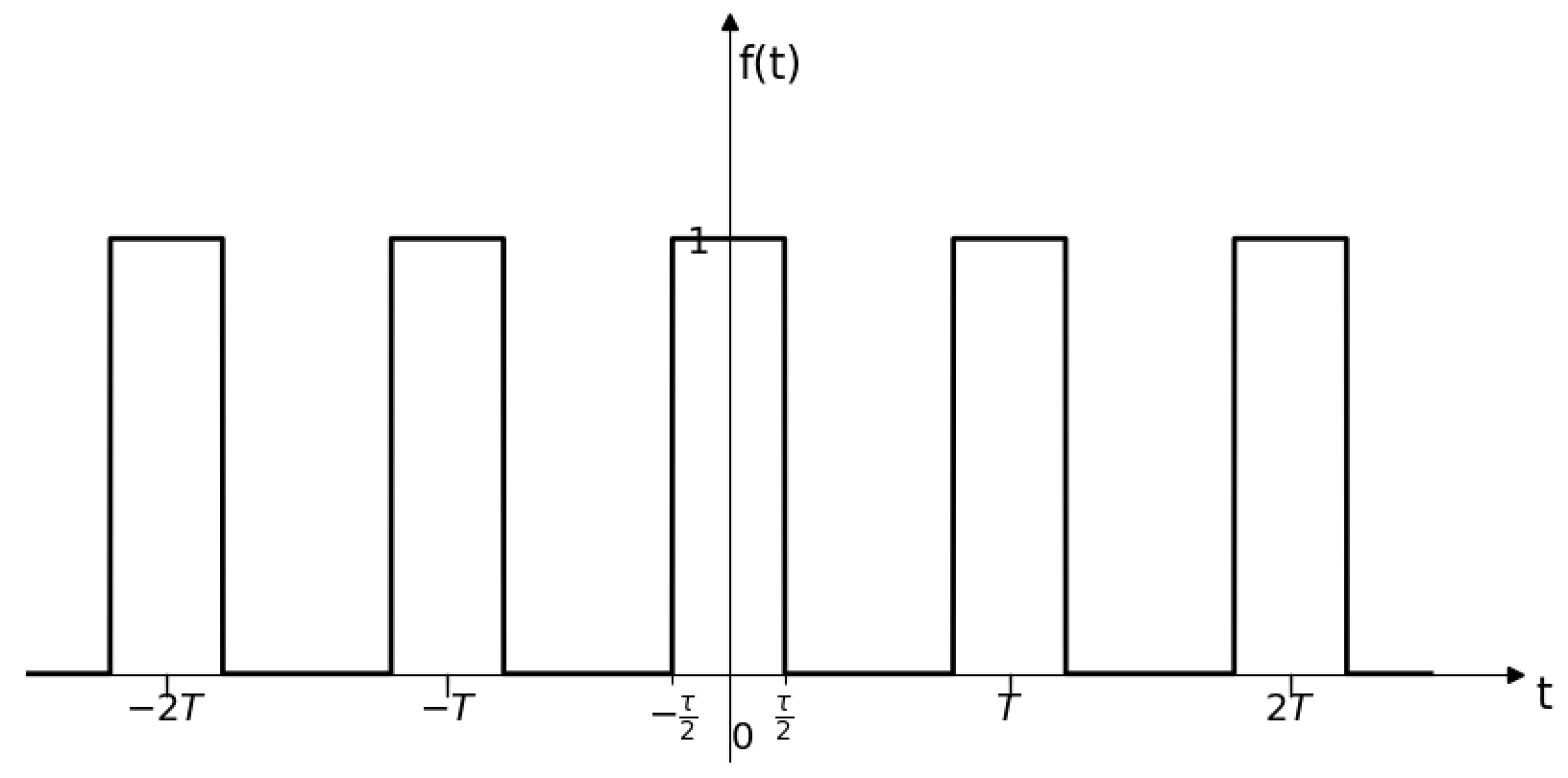
we have

$$a_k=\frac{\tau}{T}\mathrm{Sa}(\frac{k\omega_0\tau}{2})\\ \mathrm{Sa}(x)=\frac{\sin x}{x}$$

Fourier Transformation

Theory

$$X(j\omega)=\int_{-\infty}^\infty x(t)e^{-j\omega t}dt\\ x(t)=\int_{-\infty}^\infty X(j\omega)e^{j\omega t}d\omega\\$$

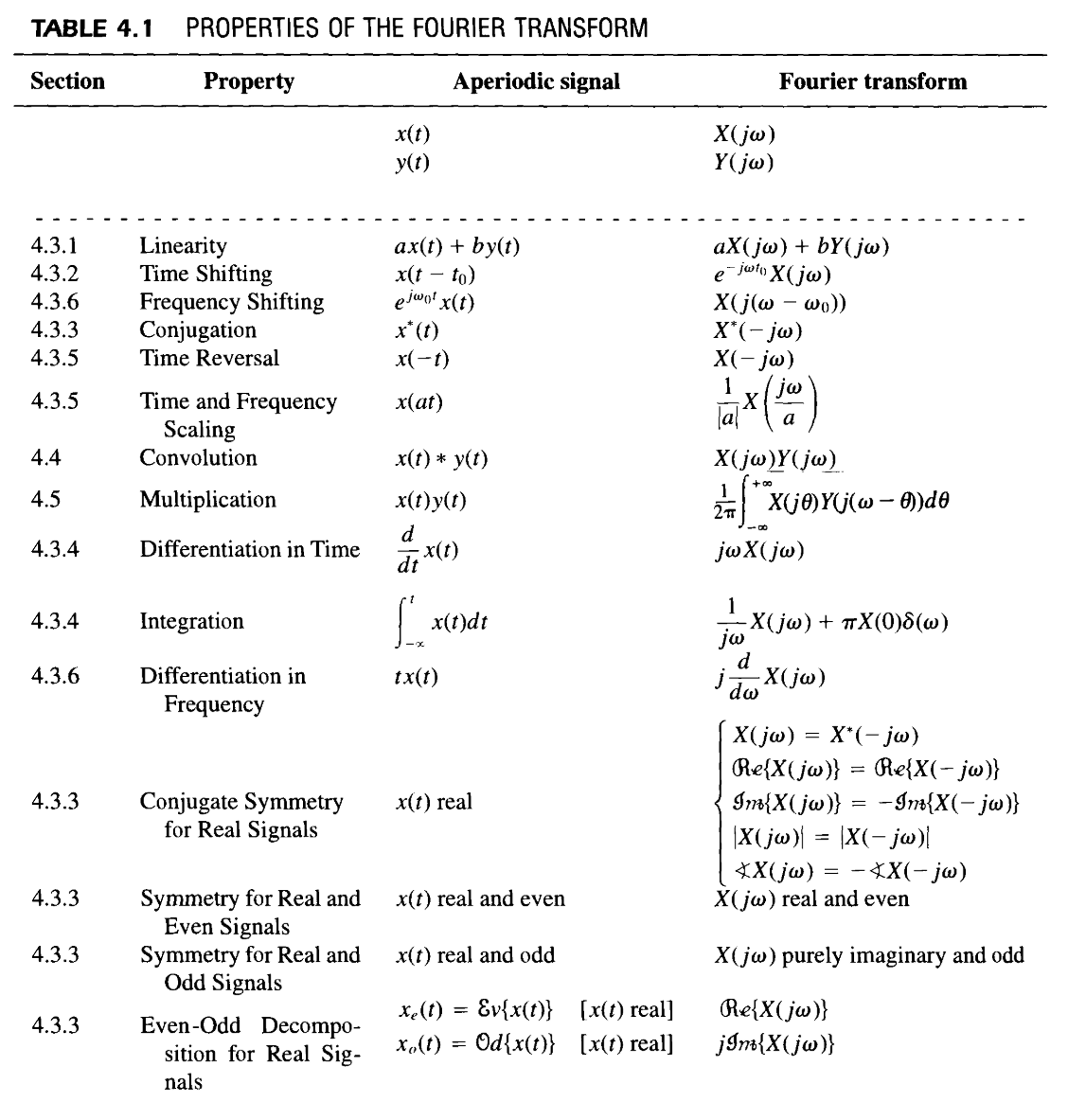
Properties

1. Linearity

   $$ax(t)+by(t)\stackrel{\mathcal{F}}{\longleftrightarrow} aX(j\omega)+bY(j\omega)$$

2. Time & frequency shifting

   $$x(t-t_0)\stackrel{\mathcal{F}}{\longleftrightarrow} e^{-j\omega t_0}X(j\omega)\\ e^{j\omega_0 t}x(t-t_0)\stackrel{\mathcal{F}}{\longleftrightarrow} X(j(\omega-\omega_0))$$

3. Conjugate symmetry

   $$x^*(t)\stackrel{\mathcal{F}}{\longleftrightarrow} X^*(-j\omega)\\ X(-j\omega)=X^*(j\omega)\quad\text{for real }x(t)$$

4. Differentiation & integration

   $$\frac{dx(t)}{dt}\stackrel{\mathcal{F}}{\longleftrightarrow}j\omega X(j\omega)\\ \int_{-\infty}^t x(\tau)d\tau\stackrel{\mathcal{F}}{\longleftrightarrow}\frac{1}{j\omega}X(j\omega)+\pi X(0)\delta(0)$$

5. Time & frequency scaling

   $$x(at)\stackrel{\mathcal{F}}{\longleftrightarrow} \frac{1}{|a|}X\left(\frac{j\omega}{a}\right)$$

6. Duality

   $$X(jt)\stackrel{\mathcal{F}}{\longleftrightarrow} 2\pi x(-\omega)$$

7. Parseval's relation

   $$\int_{-\infty}^{+\infty}|x(t)|^2dt=\frac{1}{2\pi}|X(j\omega)|^2d\omega$$

8. Convolution

   $$h(t)*x(t)\stackrel{\mathcal{F}}{\longleftrightarrow}H(j\omega)X(j\omega)\\ h(t)x(t)\stackrel{\mathcal{F}}{\longleftrightarrow}\frac{1}{2\pi}H(j\omega)*X(j\omega)$$

Fourier Transformation for Periodical Signals

A periodical signal can be expressed in terms of Fourier series as

$$x(t)=\sum_{k=-\infty}^{+\infty}a_ke^{jk\omega_0t}$$

If Fourier transformation is applied to both sides

$$\begin{aligned} X(j\omega)&=\sum_{k=-\infty}^{+\infty}a_k \mathcal{F}(e^{jk\omega_0t})\\ &=2\pi\sum_{k=-\infty}^{+\infty}a_k\delta(\omega-k\omega_0) \end{aligned}$$

As a example, we may calculate the Fourier transformation of a periodical pulse signal $\delta_T(t)=\sum_{k=-\infty}^{\infty}\delta(t-kT)$

$$\mathcal{F}[\delta_T(t)]=\omega_0\sum_{k=-\infty}^{+\infty}\delta(\omega-k\omega_0)$$

Example

Square pulse

$$x(t)= \begin{cases} 1& -\tau/2<t<\tau/2\\ 0& \text{else} \end{cases}\\ X(j\omega)=\tau\mathrm{Sa}(\frac{\omega\tau}{2})$$

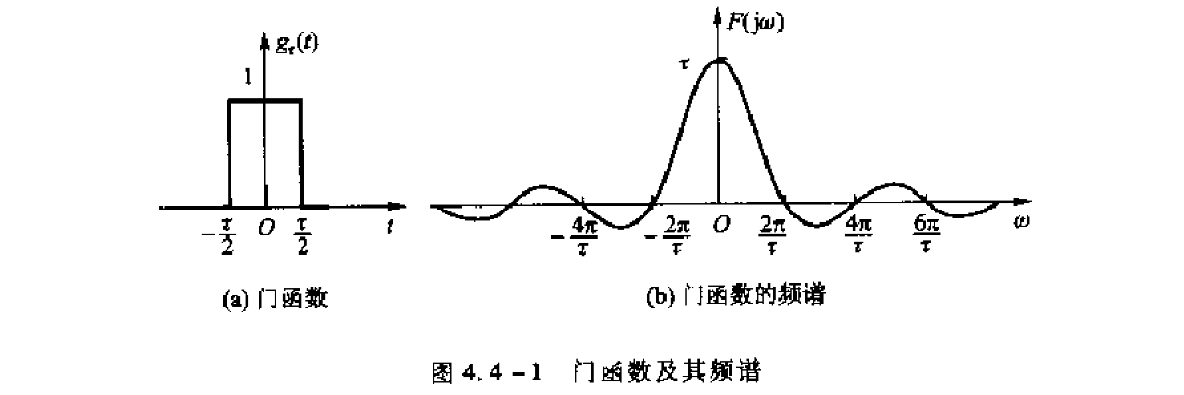
we may conclude by comparing with previous example that Fourier series coefficient can be drawn by Fourier transformation with

$$a_k=\frac{1}{T}X(jk\omega_0)$$

Discrete Time Fourier Transformation

$$x[n]=\frac{1}{2\pi}\int_{2\pi}X(e^{j\omega})e^{j\omega n}d\omega\\ X(e^{j\omega})=\sum_{k=-\infty}^{+\infty}x[n]e^{-j\omega n}$$

Laplace Transformation

$$X(s)=\int_{-\infty}^{\infty} x(t)e^{-st}dt\\ x(t)=\frac{1}{2\pi j}\int_{\sigma-j\infty}^{\sigma+j\infty} X(s)e^{st}ds$$

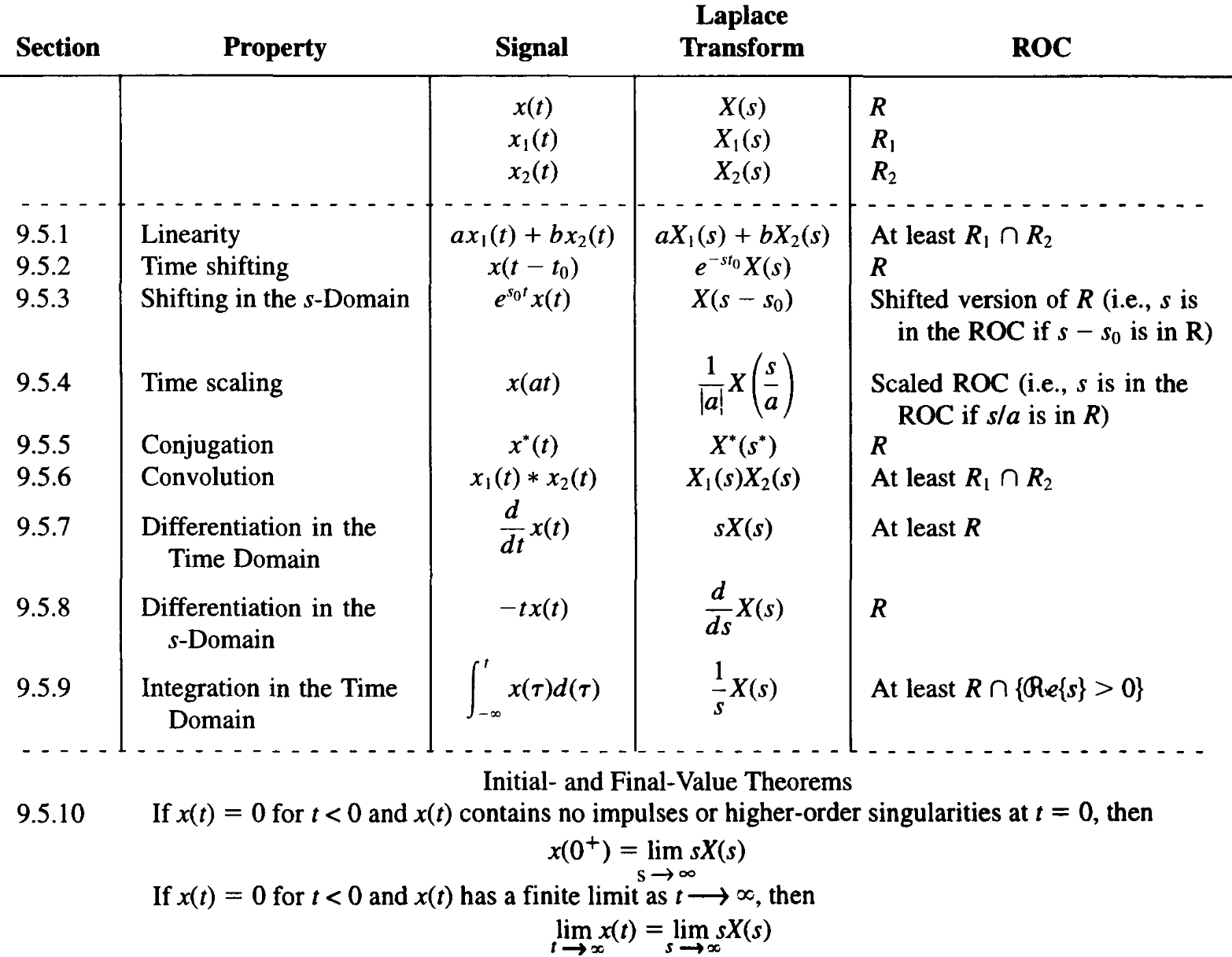
Region of convergence (ROC)

• The ROC of X(s) consists of strips parallel to the $j\omega$-axis in the s-plane.
• For rational Laplace transforms, the ROC does not contain any poles.
• If x(t) is of finite duration and is absolutely integrable, then the ROC is the entire s-plane.
• If x(t) is right sided, and if the line $\mathcal{Re}\{s\}=\sigma_0$ is in the ROC, then all values of s for which $\mathcal{Re}\{s\}>\sigma_0$ will also be in the ROC.
• If x(t) is left sided, and if the line $\mathcal{Re}\{s\}=\sigma_0$ is in the ROC, then all values of s for which $\mathcal{Re}\{s\}<\sigma_0$ will also be in the ROC.
• If x(t) is two sided, and if the line $\mathcal{Re}\{s\}=\sigma_0$ is in the ROC, then the ROC will consist of a strip in the s-plane that includes the line $\mathcal{Re}\{s\}=\sigma_0$.
• If the Laplace transform X(s) of x(t) is rational, then its ROC is bounded by poles or extends to infinity. In addition, no poles of X(s) are contained in the ROC.
• If the Laplace transform X(s) of x(t) is rational, then:
  • If x(t) is right sided, the ROC is the region in the s-plane to the right of the rightmost pole.
  • If x(t) is left sided, the ROC is the region in the s-plane to the left of the leftmost pole.

Note on expansion, for

$$F(s)=\frac{B(s)}{A(s)}=\frac{b_n s^n+...+b_1s+b_0}{a_ms^m+...+a_1s+a_0}$$

we need to solve the roots of $A(s)=0$

• For single root

  $$F(s)=\sum_{i=1}^{n} \frac{K_i}{s-s_i}$$

  where

  $$K_i=\lim_{s\to s_i}(s-s_i)\frac{B(s)}{A(s)}\\ =\frac{B(s_i)}{A'(s_i)}$$

• For conjugate roots

  $$\begin{aligned} F(s)&=\frac{B(s)}{(s-s_1)(s-s_1^*)A(s)}\\ &=\frac{K_1}{s-s_1}+\frac{K_2}{s-s_1^*}+\frac{B_2(s)}{A_2(s)} \end{aligned}$$

  where

  $$K_1=K_2^*$$

• For multiple roots

  $$\begin{aligned} F(s)&=\frac{B(s)}{(s-s_1)^rA(s)}\\ &=\frac{K_{11}}{(s-s_1)^r}+...+\frac{K_{1r}}{s-s_1}+\frac{B_2(s)}{A_2(s)} \end{aligned}$$

  where

  $$K_{1i}=\frac{1}{(i-1)!}\frac{d^{i-1}}{ds^{i-1}}[(s-s_i)^rF(s)]\bigg|_{s=s_i}$$

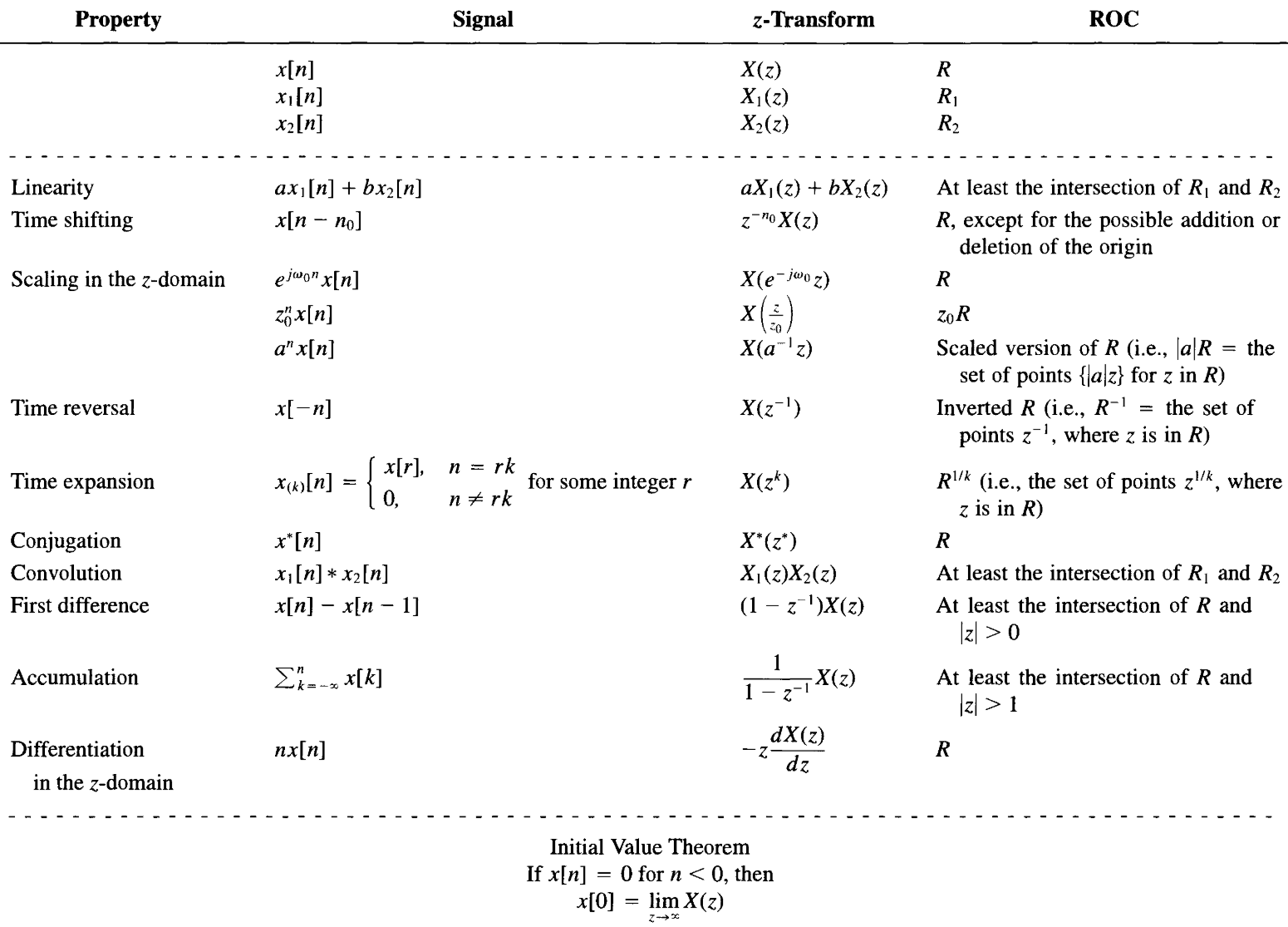
Z Transformation

$$X(z)=\sum_{k=-\infty}^{+\infty} x[n]z^{-n}\\ x[n]=\frac{1}{2\pi j}\oint X(z)z^{n-1}dz$$

ROC

• The ROC of X(z) consists of a ring in the z-plane centered about the origin.
• The ROC does not contain any poles.
• If $x[n]$ is of finite duration, then the ROC is the entire z-plane, except possibly $z=0 $ and/or $z=\infty$.
• If $x[n]$ is a right-sided sequence, and if the circle $|z|=r_0$ is in the ROC, then all finite values of z for which $|z|>r_0$ will also be in the ROC.
• If $x[n]$ is a left-sided sequence, and if the circle $|z|=r_0$ is in the ROC, then all finite values of z for which $|z|<r_0$ will also be in the ROC.
• If $x[n]$ is two sided, and if the circle $|z|=r_0$ is in the ROC, then the ROC will consist of a ring in the z-plane that includes the circle $|z|=r_0$.
• If the z-transform $X(z)$ of $x[n]$ is rational, then its ROC is bounded by poles or extends to infinity.
• If the z-transform $X(z)$ of $x[n]$ is rational,
  • If $x[n]$ is right sided, then the ROC is the region in the z-plane outside the outermost pole. Furthermore, if $x[n]$ is causal, then the ROC also includes $z=\infty$.
  • If $x[n]$ is left sided, then the ROC is the region in the z-plane inside the innermost nonzero pole. Furthermore, if $x[n]$ is anti-causal, then the ROC also includes $z=0$.

Discrete Fourier Transformation

$$X(k)=\sum_{n=0}^{N-1} x(n)e^{-j2\pi kn/N}\\ x(n)=\frac{1}{N}\sum_{k=0}^{N-1} X(k)e^{j2\pi kn/N}$$

Reference

1. 管致中, et al. 信号与线性系统，第五版.
2. Alan V. Oppenheim, et al. Signals and Systems, Second Edition.